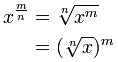Auch als „Radikale“ oder „rationale Exponenten“ bezeichnet
Exponenten für ganze Zahlen
Betrachten wir zunächst die ganze Zahl Exponenten:

Der Exponent einer Zahl gibt an, wie oft die Zahl verwendet werden soll in einer Multiplikation.
In diesem Beispiel: 82 = 8 × 8 = 64
bezeichnet werden. Ein weiteres Beispiel: 53 = 5 × 5 × 5 = 125
Bruchexponenten
Aber was ist, wenn der Exponent ein Bruch ist?
|
Ein Exponent von 12 ist tatsächlich Quadratwurzel Ein Exponent von 13 ist Kubikwurzel Ein Exponent von 14 ist die 4. Wurzel und so weiter! |
 |
Warum?
Lassen Sie uns sehen, warum in einem Beispiel.
Zunächst sagen uns die Exponentengesetze, wie wir mit Exponenten umgehen sollen, wenn wir multiplizieren:
Beispiel: x2x2 = (xx) (xx) = xxxx = x4
Was zeigt, dass x2x2 = x (2 + 2) = x4
Versuchen wir das also mit gebrochenen Exponenten:
Versuchen Sie es mit einem anderen Bruch
Versuchen wir das noch einmal, aber mit einem Exponenten von einem Viertel (1/4):
Beispiel:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Also 16¼, das viermal in einer Multiplikation verwendet wird, ergibt 16,
und somit ist 16¼ a 4. Wurzel von 16
Allgemeine Regel
Es funktionierte für ½, es funktionierte mit ¼, tatsächlich funktioniert es im Allgemeinen:
x1 / n = Die n-te Wurzel von x
Wir können uns also Folgendes einfallen lassen:
| |
|
Beispiel: Was ist 271/3?
Antwort: 271/3 = ![]() 27 = 3
27 = 3
Was ist mit komplizierteren Brüchen?
Was ist mit einem gebrochenen Exponenten wie 43/2?
Das heißt wirklich, einen Würfel (3) und eine Quadratwurzel (1/2) in beliebiger Reihenfolge zu machen.
Lassen Sie mich das erklären.
Ein Bruch (wie m / n) kann in zwei Teile unterteilt werden:
- einen ganzzahligen Teil (m) und
- einen Bruch (1 / n) Teil
Da also m / n = m × (1 / n) ist, können wir dies tun:
Die Reihenfolge spielt also keine Rolle Es funktioniert auch für m / n = (1 / n) × m:
Und wir erhalten Folgendes:
| |
|
Einige Beispiele:
Beispiel : Was ist 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
oder
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
In beiden Fällen wird das gleiche Ergebnis erzielt.
Beispiel: Was ist 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
oder
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
Auf dem 2. Weg war es sicherlich einfacher!
Jetzt … Spielen Sie mit der Grafik!
Sehen Sie, wie reibungslos sich die Kurve ändert, wenn Sie mit den Brüchen in spielen Diese Animation zeigt Ihnen, dass diese Idee von Bruchexponenten gut zusammenpasst:
Dinge, die Sie versuchen sollten:
- Beginnen Sie mit m = 1 und n = 1 und nehmen Sie dann langsam zu n, damit Sie 1/2, 1/3 und 1/4 sehen können
- Versuchen Sie dann m = 2 und schieben Sie n nach oben und unten, um Brüche wie 2/3 usw.
- zu sehen Versuchen Sie nun, den Exponenten -1
- zu machen. Versuchen Sie zuletzt, m zu erhöhen, dann n zu verringern, dann m zu verringern und dann n zu erhöhen: Die Kurve sollte sich um und um
bewegen