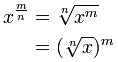Také se nazývají „radikálové“ nebo „racionální exponenti“
Exponenty celého čísla
Nejprve se podívejme na celé číslo exponenty:

exponent čísla říká, kolikrát použít číslo v násobení.
V tomto příkladu: 82 = 8 × 8 = 64
Další příklad: 53 = 5 × 5 × 5 = 125
Frakční exponenti
Ale co když je exponent zlomek?
|
exponent 12 je ve skutečnosti druhá odmocnina exponent 13 je kořenová krychle Exponent 14 je 4. kořen. A tak dále! |
 |
proč?
Pojďme vidět proč v příklad.
Nejprve nám zákony exponentů říkají, jak zacházet s exponenty, když násobíme:
Příklad: x2x2 = (xx) (xx) = xxxx = x4
Což ukazuje, že x2x2 = x (2 + 2) = x4
Zkusme to s zlomkovými exponenty:
Zkuste jinou frakci
Zkusme to znovu, ale s exponentem jedné čtvrtiny (1/4):
Příklad:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Takže 16¼ použité 4krát v násobení dává 16,
a tedy 16¼ je 4. kořen 16
Obecné pravidlo
Fungovalo to pro ½, fungovalo to pro ¼, ve skutečnosti to funguje obecně:
x1 / n = N-tý kořen x
Takže můžeme přijít s tímto:
| |
|
Příklad: Co je 271/3?
Odpověď: 271/3 = ![]() 27 = 3
27 = 3
A co složitější zlomky?
A co zlomkový exponent jako 43/2?
To ve skutečnosti znamená udělat kostku (3) a druhou odmocninu (1/2) v libovolném pořadí.
Dovolte mi to vysvětlit.
Zlomek (například m / n) lze rozdělit na dvě části:
- celá část s číslem (m) a
- zlomek (1 / n) část
Takže, protože m / n = m × (1 / n) to můžeme udělat:
Na pořadí nezáleží, takže funguje to také pro m / n = (1 / n) × m:
A dostaneme toto:
| |
|
Některé příklady:
Příklad : Co je 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
nebo
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
V obou případech bude výsledek stejný.
Příklad: Co je 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
nebo
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
Druhou cestou to bylo určitě jednodušší!
Nyní … Hrajte s grafem!
Podívejte se, jak plynule se křivka mění, když hrajete s frakcemi v tato animace, to vám ukáže, že tato myšlenka zlomkových exponentů do sebe pěkně zapadá:
Co vyzkoušet:
- Začněte s m = 1 an = 1, pak pomalu zvyšujte n tak, abyste viděli 1/2, 1/3 a 1/4
- Pak zkuste m = 2 a posunutím n nahoru a dolů zobrazte zlomky jako 2/3 atd.
- Nyní zkuste udělat exponent -1
- Nakonec zkuste zvětšit m, pak zmenšit n, pak zmenšit m, pak zvětšit n: křivka by měla jít dokola