Nyní, když jste se naučili znásobovat celá čísla, dělení celých čísel by mělo být hračkou. Důvod je ten, že se řídí stejnými pravidly.
pravidla o tom, jak rozdělit celá čísla
Krok 1: Rozdělte jejich absolutní hodnoty.
Krok 2: Určete znaménko konečné odpovědi (známé jako kvocient) pomocí následujících podmínek.
- Podmínka 1: Pokud jsou znaménka dvou čísel stejná, je kvocient vždy kladné číslo.
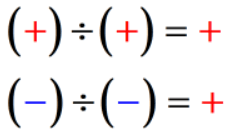
- Podmínka 2: Pokud jsou znaménka dvou čísel odlišná, podíl je vždy záporné číslo.
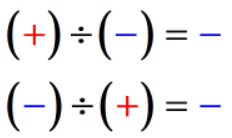
Příklady celočíselného dělení
Příklad 1: Rozdělte dvě celá čísla níže.
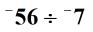
Řešení: Nejprve najděte absolutní hodnoty dvou celých čísel.
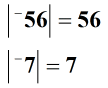
Dále rozdělte čísla nebo vyhledejte jejich podíl .
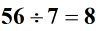
Nakonec určete konečné znaménko odpovědi nebo kvocientu. Protože rozdělujeme dvě celá čísla se stejným znaménkem, bude mít podíl kladné znaménko.
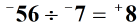
Příklad 2: Rozdělte dvě celá čísla níže.
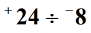
Řešení: Rozdělte absolutní hodnoty dvou celých čísel.
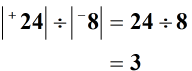
Při dělení celých čísel různými způsoby dodržujte výše uvedená pravidla podepíše, že konečná odpověď (podíl) je záporná.
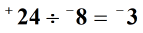
Příklad 3: Rozdělte tři celá čísla dole zleva doprava
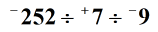
Řešení: Chcete-li rozdělit tři nebo více celých čísel, je důležité provést operaci dělení zleva doprava. Navíc toho můžeme dosáhnout dělením dvou celých čísel najednou. V závorkách jsou uvedena první dvě celá čísla, která se mají rozdělit, a jakýkoli výsledek nebo kvocient bude vydělen dalším. Takže tady máme, – 252 děleno + 7 se rovná – 36. Jde o záporný kvocient, protože dělíme dvě celá čísla, která mají různá znaménka. Pak vezmeme tento kvocient a vydělíme jej celým číslem, které následuje. Dostaneme –36 ÷ –9 = + 4.
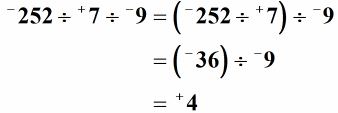
Cvičení s pracovními listy
Také by vás mohlo zajímat:
Sčítání celých čísel
Odečítání celých čísel
Násobení celých čísel