Co je standardní odchylka? | STDEV.P | STDEV.S | Odchylka
Tato stránka vysvětluje, jak vypočítat směrodatnou odchylku na základě celé populace pomocí funkce STDEV.P v aplikaci Excel a jak odhadnout směrodatnou odchylku na základě vzorku pomocí funkce STDEV.S v aplikaci Excel.
Co je standardní odchylka?
Standardní odchylka je číslo, které vám řekne, jak daleko jsou čísla od jejich průměru.
1. Například níže uvedená čísla mají průměr (průměr) 10.
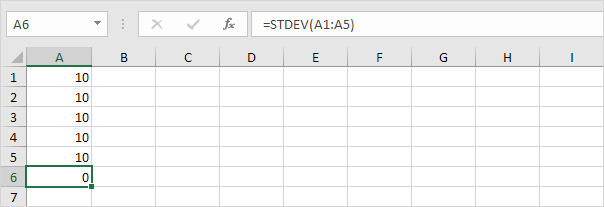
Vysvětlení: všechna čísla jsou stejná, která znamená, že neexistuje žádná variace. Výsledkem je, že čísla mají směrodatnou odchylku nula. Funkce STDEV je stará funkce. Microsoft Excel doporučuje používat novou funkci STEDV.S, která produkuje přesně stejný výsledek.
2. Níže uvedená čísla mají také průměr (průměr) 10.
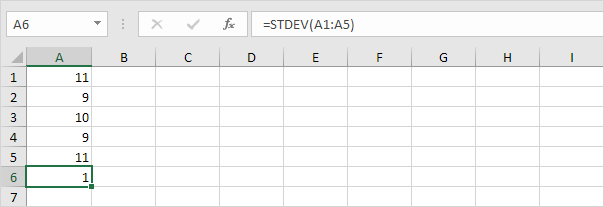
Vysvětlení: čísla jsou blízko průměru. Výsledkem je, že čísla mají nízkou směrodatnou odchylku.
3. Níže uvedená čísla mají také průměr (průměr) 10.
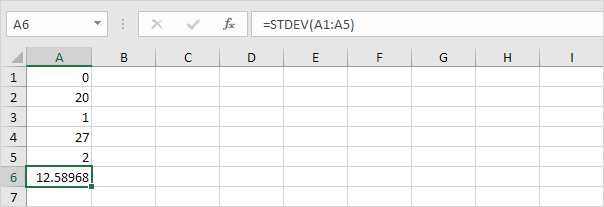
Vysvětlení: čísla jsou rozložena. Ve výsledku mají čísla vysokou standardní odchylku.
STDEV.P
Funkce STDEV.P (P znamená Population) v aplikaci Excel vypočítá směrodatnou odchylku na základě celé populace. Učíte například skupinu 5 studentů. Máte výsledky testů všech studentů. Celá populace se skládá z 5 datových bodů. Funkce STDEV.P používá následující vzorec:
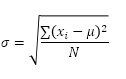
V tomto příkladu x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (průměr), N = 5 (počet datových bodů).
1. Vypočítejte průměr (μ).
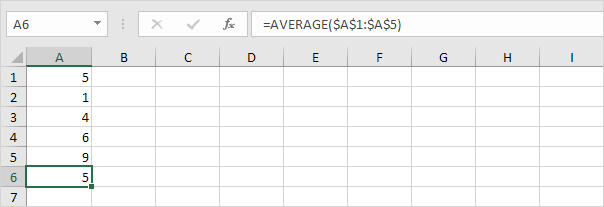
2. Pro každé číslo vypočítejte vzdálenost k průměru.
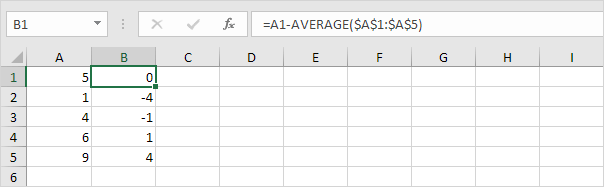
3. U každého čísla tuto vzdálenost zaokrouhlete.
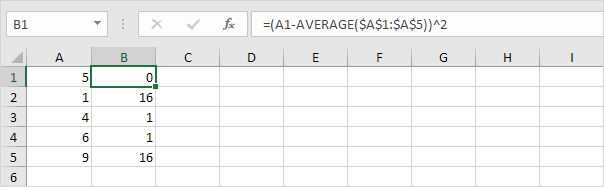
4. Součet (∑) těchto hodnot.
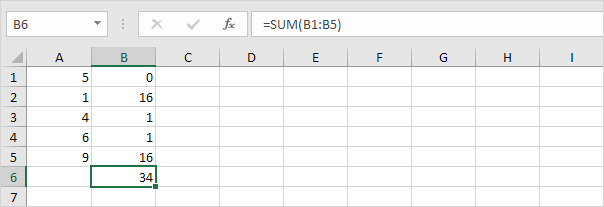
5. Vydělte počtem datových bodů (N = 5).
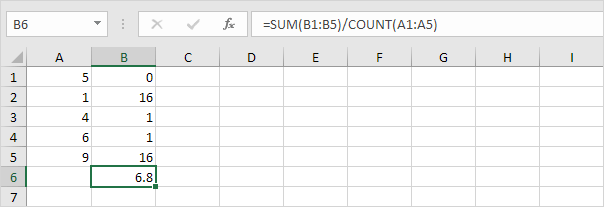
6. Vezměte odmocninu.
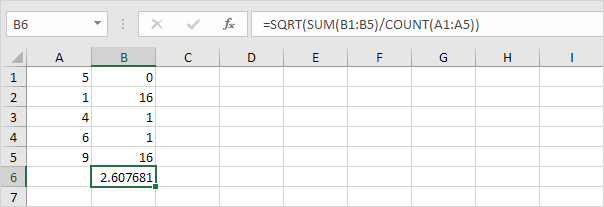
7. Naštěstí může funkce STDEV.P v aplikaci Excel provést všechny tyto kroky za vás.
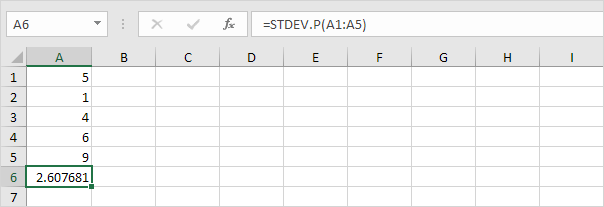
STDEV.S
Funkce STDEV.S (S znamená Sample) v aplikaci Excel odhaduje standardní odchylku na základě vzorku. Například učíte velkou skupinu studentů. Máte pouze testovací skóre 5 studentů. Velikost vzorku se rovná 5. Funkce STDEV.S používá následující vzorec:
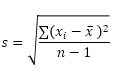
V tomto příkladu x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (stejná čísla jako výše), x̄ = 5 (ukázka průměr), n = 5 (velikost vzorku).
1. Opakujte kroky 1-5 výše, ale v kroku 5 vydělte n-1 místo N.
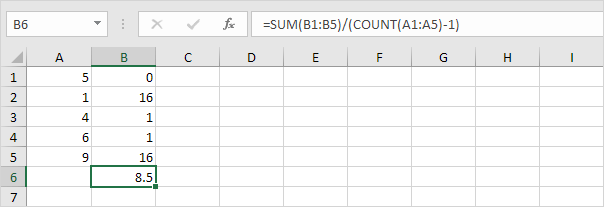
2. Vezměte druhou odmocninu.
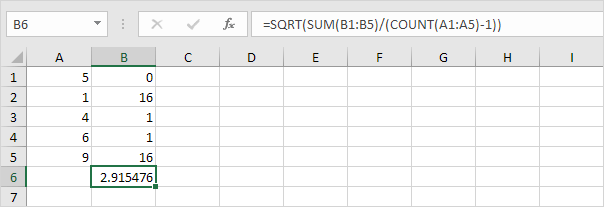
3. Naštěstí může funkce STDEV.S v aplikaci Excel provést všechny tyto kroky za vás.
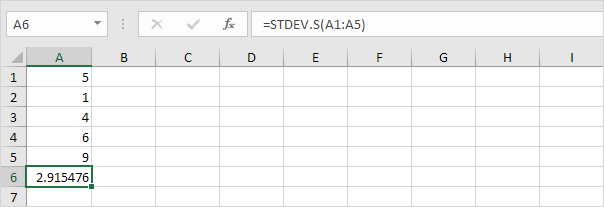
Poznámka: proč dělíme podle n – 1 místo n, když odhadujeme směrodatnou odchylku na základě vzorku? Besselova korekce uvádí, že vydělením n-1 místo n získáme lepší odhad směrodatné odchylky.
Rozptyl
Odchylka je druhou mocninou směrodatné odchylky. Je to tak jednoduché. Někdy je jednodušší použít rozptyl při řešení statistických problémů.
1. Níže uvedená funkce VAR.P vypočítá rozptyl na základě celé populace.
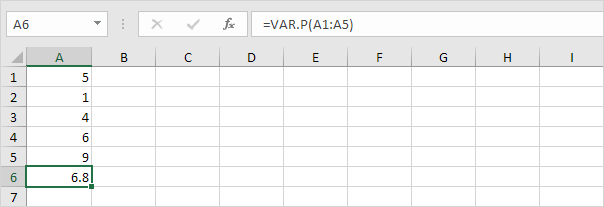
Poznámka: tuto odpověď jste již znali (viz krok 5 pod STDEV.P). Z druhé odmocniny tohoto výsledku vyhledejte směrodatnou odchylku na základě celé populace.
2. Níže uvedená funkce VAR.S odhaduje rozptyl na základě vzorku.
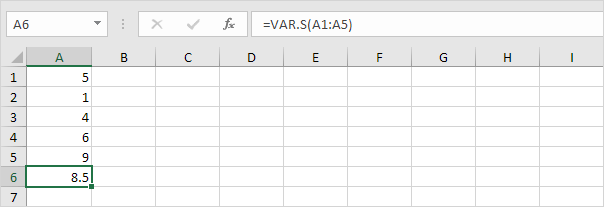
Poznámka: tuto odpověď jste již znali (viz krok 1 pod STDEV.S). Na základě odmocniny tohoto výsledku vyhledejte směrodatnou odchylku na základě vzorku.
3. VAR a VAR.S produkují přesně stejný výsledek.
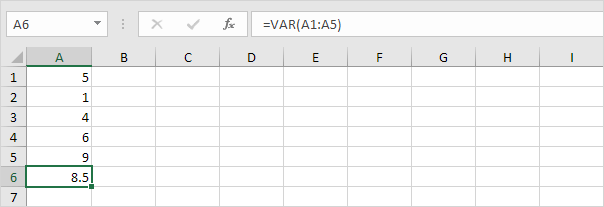
Poznámka: Microsoft Excel doporučuje používat novou funkci VAR.S.