Poincarého domněnka a dalších 6 složitých matematických teorií byly pojmenovány Problémy s cenou tisíciletí Clay Mathematics Institute (CMI). Každý problém byl popsán jako „důležitá klasická otázka, která v průběhu let odolávala řešením“, přičemž první osoba, která navrhla řešení pro každého, vydělala 1 000 000 $ s laskavým svolením CMI. Jak jste však viděli výše, řešení těchto problémů není snadné feat. Jeden z problémů zůstal nevyřešen, protože byl vytvořen v roce 1859 německým matematikem Bernhardem Riemannem.
Riemannova hypotéza, pojmenovaná po výše zmíněném německém matematikovi, je obecně považována za nejdůležitější nevyřešený problém v čistém matematika. Teorie čísel má velký zájem, protože implikuje výsledky distribuce prvočísla, které se používají ve všem od biologie po šifrování a kvantovou mechaniku. Abychom porozuměli Riemannově hypotéze, je třeba nejprve vysvětlit několik klíčových koncepty:
- Komplexní číslo má tvar a + bi, kde i je definováno pomocí i² = -1. V tomto tvaru je skutečná část komplexního čísla a a imaginární část je bi.
- Funkce Riemannova zeta je funkcí komplexní proměnné (funkce komplexních čísel) definované následující rovnicí, kde s je jakékoli komplexní číslo jiné než 1 a jehož hodnoty jsou také komplexní:
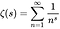
- „Nula“ funkce je x takové, že f (x) = 0
- „triviální nuly“ funkce Riemannova zeta jsou všechna záporná sudá celá čísla (-2, -4, -6,…)
- „netriviální nuly ”Funkce Riemannova zeta jsou všechny ostatní hodnoty s, pro které ζ (s) = 0 (tj. s není záporné sudé celé číslo).
Nyní, když máme několik definic dolů, můžeme pokračovat a vyslovit Riemannovu hypotézu:
Skutečná část každé netriviální nuly funkce Riemann zeta je 1/2
Tato (pro mě přinejmenším) je mnohem snazší pochopit než Poincarého dohad a nezdá se intuitivně příliš obtížný. Nezdá se však, že by to znamenalo mnoho. Opravdu, koho zajímá, když má tato náhodná funkce hodnotu 0. Není divu, že to dělá spousta matematiků, a to z velmi dobrého důvodu.
Některá čísla mají zvláštní vlastnost, že je nelze vyjádřit jako produkt dvou menších čísel (produkt se množí), tj. 2,3,5,7,11 atd. Známá jako prvočísla, jsou v jistém smyslu nejjednodušší čísla, která můžete získat, tvořící stavební kameny pro všechna ostatní čísla. Frustrující je však to, že se zdá, že prvočísla nenásledují žádný vzorec. 3137 je prvočíslo a další po něm bude až do roku 3163, ale poté následují 3167 a 3169 v rychlém sledu, což jsou všechna prvočísla. Stručně řečeno, pokud najdete jedno prvočíslo, neexistuje žádný způsob, jak zjistit, kde bude další, aniž byste při procházení zkontrolovali všechna čísla. Pomocí věty o prvočíslech (PNT) však můžete zjistit, kolik prvočísel je pod určitou prahovou hodnotou.
Věta o prvočíslech je pouze odhad, přičemž různé hodnoty dávají jinou pravděpodobnost, že budou správné, ale nikdy 100% jistota. Pochopte však předpoklad, že Reimannova hypotéza je pravdivá, můžete vytvořit matematickou aproximaci kombinující teorém o prvém čísle a netriviální nuly funkce Riemannova zeta, aby se opravily chyby vnitřních komponent a poskytly se „nejlepší možné“ hranice pro chybový termín v teorému prvočísla. Pokud by bylo možné zcela dokázat Reimannovu hypotézu, dalo by to PNT schopnost poskytovat neuvěřitelně blízké odhady skutečné hodnoty, což by otevíralo mnoho možností v různých oborech matematiky. existuje mnoho důležitých hypotéz, které jsou s „Pokud je Riemannova hypotéza pravdivá, pak…“, takže řešení tohoto problému by okamžitě potvrdilo i všechny následující dohady.