Vergessen Sie alles, was Sie über Zahlen wissen.
Vergessen Sie in der Tat, dass Sie sogar wissen, was eine Zahl ist.
Dies Hier beginnt die Mathematik.
Anstelle von Mathematik mit Zahlen werden wir jetzt über Mathematik mit „Dingen“ nachdenken.
Definition
Was ist ein Set? Einfach gesagt, es ist eine Sammlung.
Zuerst geben wir eine gemeinsame Eigenschaft unter „Dingen“ an (wir definieren dieses Wort später) und sammeln dann alle „Dinge“, die diese gemeinsame Eigenschaft haben.

Zum Beispiel die Artikel, die Sie tragen: Hut, Hemd, Jacke, Hose und so weiter.
Ich bin sicher, Sie könnten sich mindestens hundert einfallen lassen.
Dies wird als Menge bezeichnet.
|
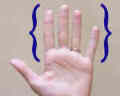
Oder ein anderes Beispiel sind Fingertypen. Dieser Satz enthält Index, Mitte und Ring und pinky. |
 |
Es handelt sich also nur um Dinge, die mit einer bestimmten Eigenschaft gemeinsam gruppiert sind.
Notation
Es gibt eine ziemlich einfache Notation für Mengen. Wir listen einfach jedes Element (oder „Mitglied“) auf, das durch ein Komma getrennt ist, und setzen dann einige geschweifte Klammern um das Ganze:

Die geschweiften Klammern {} werden manchmal als „Klammern setzen“ oder „Klammern“ bezeichnet.
Dies ist die Notation für die beiden vorherigen Beispiele:
{Socken, Schuhe, Uhren, Hemden, …}
{Index, Mitte, Ring, kleiner Finger}
Beachten Sie, wie das erste Beispiel das „…“ hat (drei Punkte zusammen)
Die drei Punkte … werden als Auslassungspunkte bezeichnet und bedeuten „weiter“.
Das heißt, das erste Beispiel wird fortgesetzt. . für die Unendlichkeit.
(OK, es gibt nicht wirklich unendlich viele Dinge, die man tragen könnte, aber da bin ich mir nicht ganz sicher! Nach einer Stunde des Nachdenkens über verschiedene Dinge bin ich es Ich bin mir immer noch nicht sicher. Sagen wir einfach, dass es für dieses Beispiel unendlich ist.)
Also:
Aber manchmal kann das „…“ in der Mitte zum Speichern verwendet werden Schreiben langer Listen:
Beispiel: Der Satz von Buchstaben:
{a, b, c, .. ., x, y, z}
In diesem Fall handelt es sich um eine endliche Menge (es gibt nur 26 Buchstaben, richtig?)
Numerische Mengen
Was hat das mit Mathematik zu tun? Wenn wir eine Menge definieren, müssen wir nur ein gemeinsames Merkmal angeben. Wer sagt, dass wir dies mit Zahlen nicht tun können?
Und so weiter. Wir können uns alle Arten von Mengen einfallen lassen.
Wir können eine Menge auch anhand ihrer Eigenschaften definieren. Beispiel: {x | x > 0}, was „die Menge aller x“ bedeutet, sodass x größer als 0 ist. Weitere Informationen finden Sie unter Set-Builder-Notation.
Und wir können Sätze von Zahlen haben, die keine gemeinsame Eigenschaft haben, sie werden nur so definiert. Zum Beispiel:
{4, 5, 6, 10, 21}
{2, 949, 48282, 42882959, 119484203 }
Sind alle Mengen, die ich zufällig auf meine Tastatur gedrückt habe, um sie zu erzeugen.
Warum sind Mengen wichtig?
Mengen sind die grundlegende Eigenschaft der Mathematik. Nun, als ein Wort der Warnung, scheinen Sets für sich genommen ziemlich sinnlos. Aber nur wenn wir Mengen in verschiedenen Situationen anwenden, werden sie zum mächtigen Baustein der Mathematik.
Mathematik kann ziemlich schnell erstaunlich kompliziert werden. Graphentheorie, Abstrakte Algebra, Reale Analyse, Komplex Analyse, lineare Algebra, Zahlentheorie und die Liste gehen weiter. Eines haben alle gemeinsam: Mengen.
Universelle Menge
 |
Am Anfang haben wir das Wort „Dinge“ in Anführungszeichen verwendet. Wir nennen dies die universelle Menge. Es ist eine Menge, die alles enthält. Nun, nicht genau alles. Alles, was für unsere Frage relevant ist. |
|
 |
In der Zahlentheorie besteht die universelle Menge aus allen ganzen Zahlen, da die Zahlentheorie einfach die ist Untersuchung von ganzen Zahlen. |
|
 |
In Calculus (auch als reelle Analyse bezeichnet) besteht die universelle Menge fast immer aus den reellen Zahlen. |
|
 |
Und in der komplexen Analyse haben Sie es erraten, die universelle Menge sind die komplexen Zahlen. |
Weitere Notation
 |
Wenn es um Mengen geht, ist es ziemlich üblich, Großbuchstaben zur Darstellung der Menge und Kleinbuchstaben zur Darstellung zu verwenden ein Element in dieser Menge. So ist beispielsweise A eine Menge und a ein Element nt in A. Gleich mit B und b und C und c. |
Jetzt müssen Sie nicht mehr auf den Standard hören Sie können so etwas wie m verwenden, um eine Menge darzustellen, ohne gegen mathematische Gesetze zu verstoßen (Achtung, Sie können π Jahre im Mathe-Gefängnis erhalten, wenn Sie durch 0 teilen), aber diese Notation ist ziemlich nett und leicht zu befolgen. Warum also nicht?
Wenn wir sagen, dass sich ein Element a in einer Menge A befindet, verwenden wir das Symbol ![]() , um es anzuzeigen.
, um es anzuzeigen.
Und wenn sich etwas nicht in a befindet set use ![]() .
.
Beispiel: Set A ist {1,2,3}. Wir können sehen, dass 1 ![]() A, aber 5
A, aber 5 ![]() A
A
Gleichheit
Zwei Mengen sind gleich, wenn sie genau die haben gleiche Mitglieder. Nun, auf den ersten Blick scheinen sie nicht gleich zu sein, daher müssen wir sie möglicherweise genau untersuchen!
Beispiel: Sind A und B gleich, wobei:
- A ist die Menge, deren Mitglieder die ersten vier positiven ganzen Zahlen sind.
- B = {4, 2, 1, 3}
Überprüfen wir. Sie enthalten beide 1. Sie enthalten beide 2. und 3 und 4. Und wir haben jedes Element beider Mengen überprüft, also: Ja, sie sind gleich!
Und das Gleichheitszeichen ( =) wird verwendet, um Gleichheit zu zeigen, also schreiben wir:
A = B

Teilmengen
Wenn wir eine Menge definieren und Teile dieser Menge nehmen, können wir eine sogenannte Teilmenge bilden.
Im Allgemeinen:
A ist genau dann eine Teilmenge von B, wenn sich jedes Element von A in B befindet.
Verwenden wir diese Definition also in einigen Beispielen.
Versuchen wir es mit einem härteren Beispiel.
Richtige Teilmengen
Wenn wir uns die Definition von Teilmengen ansehen und unsere Gedanken ein wenig schweifen lassen, kommen wir zu einem seltsamen Punkt Schlussfolgerung.
Sei A eine Menge. Ist jedes Element von A in A?
Nun, ähm, ja natürlich, richtig?
Das bedeutet also, dass A eine Teilmenge von A ist. Es ist eine Teilmenge von sich selbst!
Dies scheint nicht sehr richtig zu sein, oder? Wenn wir wollen, dass unsere Teilmengen richtig sind, führen wir (was anderes als) richtige Teilmengen ein:
A ist genau dann eine richtige Teilmenge von B. Element von A ist auch in B, und es gibt mindestens ein Element in B, das nicht in A ist.
Dieses kleine Stück am Ende ist da, um sicherzustellen, dass A nicht a ist richtige Teilmenge von sich selbst: Wir sagen, dass B mindestens ein zusätzliches Element haben muss.
Beispiel:
{1, 2, 3} ist eine Teilmenge von {1, 2, 3}, ist aber keine richtige Teilmenge von {1, 2, 3}.
Beispiel:
{1, 2, 3} ist eine richtige Teilmenge von {1, 2, 3, 4}, da sich das Element 4 nicht in der ersten Menge befindet.
Beachten Sie, dass A auch eine richtige Teilmenge von B ist eine Teilmenge von B.
Noch mehr Notation
Wenn wir sagen, dass A eine Teilmenge von B ist, schreiben wir A ![]() B.
B.
Oder wir kann sagen, dass A keine Teilmenge von B ist durch A ![]() B („A ist keine Teilmenge von B“)
B („A ist keine Teilmenge von B“)
Wenn wir über richtige Teilmengen sprechen, Wir nehmen die darunter liegende Linie heraus und so wird sie zu A ![]() B oder, wenn wir das Gegenteil sagen wollen, zu A
B oder, wenn wir das Gegenteil sagen wollen, zu A ![]() B.
B.
Leerer (oder Null-) Satz
Dies ist wahrscheinlich das Seltsamste an Sätzen.

Stellen Sie sich als Beispiel die Klaviertasten einer Gitarre vor.
„Aber warten Sie!“ Sie sagen: „Es gibt keine Klaviertasten auf einer Gitarre! „
Und richtig, Sie sind. Es ist eine Menge ohne Elemente.
Dies wird als leere Menge (oder Nullmenge) bezeichnet. Es sind keine Elemente darin. Nicht eine. Null.
Es wird dargestellt durch ![]()
oder durch {} (eine Menge ohne Elemente)
Einige andere Beispiele für die leere Menge sind die Menge von Ländern südlich des Südpols.
Was ist also so seltsam an dem leeren Set? Nun, dieser Teil kommt als nächstes.
Leere Menge und Teilmengen
Kehren wir also zu unserer Definition von Teilmengen zurück. Wir haben eine Menge A. Wir werden sie nicht definieren mehr als das, es könnte jeder Satz sein. Ist die leere Menge eine Teilmenge von A?
Zurück zu unserer Definition von Teilmengen: Wenn jedes Element in der leeren Menge auch in A ist, dann ist die leere Menge eine Teilmenge von A. Aber was ist, wenn wir Haben Sie keine Elemente?
Um dies zu verstehen, ist eine Einführung in die Logik erforderlich, aber diese Aussage ist „vakuum“ oder „trivial“ wahr.
Eine gute Möglichkeit, darüber nachzudenken es ist: Wir können keine Elemente in der leeren Menge finden, die nicht in A sind, also muss es sein, dass alle Elemente in der leeren Menge in A sind.
Also die Antwort auf die gestellte Frage ist ein klares Ja.
Die leere Menge ist eine Teilmenge jeder Menge, einschließlich der leeren Menge selbst.
Reihenfolge
Nein, nicht die Reihenfolge der Elemente. In Mengen spielt es keine Rolle, in welcher Reihenfolge sich die Elemente befinden.
Beispiel: {1,2,3,4} ist dieselbe Menge wie {3,1,4,2}
Wenn wir Reihenfolge in Mengen sagen, meinen wir die Größe der Menge.
Ein anderer (besserer) Name hierfür ist Kardinalität.
Eine endliche Menge hat eine endliche Ordnung (oder Kardinalität). Eine unendliche Menge hat eine unendliche Ordnung (oder Kardinalität).
Bei endlichen Mengen ist die Reihenfolge (oder Kardinalität) die Anzahl der Elemente.
Beispiel: {10, 20, 30, 40} hat eine Reihenfolge von 4.
Für unendliche Mengen können wir nur sagen, dass die Reihenfolge unendlich ist. Seltsamerweise können wir mit Mengen sagen, dass einige Unendlichkeiten größer sind als andere, aber dies ist ein fortgeschritteneres Thema in Mengen.
Arg! Nicht mehr Notation!
Nein, nur ein Scherz. Keine Notation mehr.
von
und