Poincarén oletus ja 6 muuta monimutkaista matemaattista teoriaa on kutsuttu Clay Mathematics Institute (CMI) Millennium Prize -ongelmiksi. Jokaista ongelmaa on kuvattu ”tärkeäksi klassiseksi kysymykseksi, joka on vastustanut ratkaisuja vuosien varrella”, ja ensimmäinen henkilö suunnitteli ratkaisun kullekin ansaitsemaan 1 000 000 dollaria CMI: n luvalla. Kuten edellä näet, näiden ongelmien ratkaiseminen ei ole helppoa feat. Yksi ongelmista on jäänyt ratkaisematta siitä lähtien, kun saksalaisen matemaatikon Bernhard Riemannin muotoili sen vuonna 1859.
Riemannin hypoteesia, joka on nimetty edellä mainitun saksalaisen matemaatikon mukaan, pidetään yleisesti tärkeimpänä puhtaana ongelmana. matematiikka. Se on erittäin kiinnostava lukuteoriasta, koska se merkitsee tuloksia alkuluvun jakautumisesta, joita käytetään kaikessa biologiasta salaukseen ja kvanttimekaniikkaan. Riemannin hypoteesin ymmärtämiseksi meidän on ensin selitettävä muutama avain käsitteet:
- Kompleksiluku on muodoltaan a + bi, jossa i määritetään i² = -1. Tässä muodossa kompleksiluvun todellinen osa on a ja imaginaarinen osa on bi.
- Riemannin zeta-funktio on seuraavan yhtälön määrittämän kompleksimuuttujan (kompleksilukujen funktio) funktio, jossa s on mikä tahansa muu kompleksiluku kuin 1 ja jonka arvot ovat myös monimutkaiset:
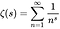
- Funktion ”nolla” on x, joka f (x) = 0
- Riemannin zeta-funktion ”triviaalit nollat” ovat kaikki negatiivisia parillisia kokonaislukuja (-2, -4, -6,…)
- ”Ei-triviaalit nollat” Riemannin zeta-funktion ”kaikki muut s-arvot, joille ζ (s) = 0 (ts. s ei ole negatiivinen parillinen kokonaisluku).
Nyt kun meillä on joitain määritelmiä alaspäin, voimme jatkaa ja lausua Riemannin hypoteesin:
Riemannin zeta-funktion jokaisen ei-triviaalin nollan todellinen osa on 1/2
Tämä (minulle Ainakin) on paljon helpommin ymmärrettävissä kuin Poincarén arvelu, eikä se näytä intuitiivisesti kovin vaikealta. Se ei myöskään näytä tarkoittavan paljon. Oikeasti, kuka välittää, kun tämän satunnaisfunktion arvo on 0. Ei ole yllättävää, että monet matemaatikot tekevät, ja erittäin hyvästä syystä.
Joillakin numeroilla on erityinen ominaisuus, jota ei voida ilmaista kahden pienemmän luvun tulona (tuote on kertolasku), ts. 2,3,5,7,11 jne. Tunnetaan alkulukuina, ja ne ovat tavallaan yksinkertaisimmat luvut, jotka saat, muodostaen rakennuspalikat kaikille muille numeroille. Turhauttavasti kuitenkin alkuluvut eivät näytä noudattavan mitään mallia. 3137 on alkuluku, ja seuraava sen jälkeen on vasta 3163, mutta sitten 3167 ja 3169 seuraavat nopeasti peräkkäin, jotka kaikki ovat primejä. Lyhyesti sanottuna, jos löydät yhden alkuluvun, ei ole mitään tapaa kertoa, missä seuraava tulee olemaan tarkistamatta kaikkia numeroita mennessäsi. Käyttämällä Prime Number Theorem (PNT) -sovellusta voit kuitenkin selvittää, kuinka monta alkulukua tietyn kynnyksen alapuolella on.
Prime Number Theorem on vain arvio, jossa eri arvot antavat erilaisen todennäköisyyden olla oikein, mutta ei koskaan 100% varmuutta. Ymmärrä kuitenkin oletus, että Reimannin hypoteesi on totta, voit luoda matemaattisen likiarvon, joka yhdistää alkuluku-lauseen ja Riemannin zeta-funktion ei-triviaaliset nollat sisäisten komponenttien virhekorjaamiseksi, jolloin saadaan ”paras mahdollinen” virheen termi päälukulauseessa. Jos Reimannin hypoteesi olisi mahdollista todistaa kokonaan, se antaisi PNT: lle mahdollisuuden tarjota uskomattoman lähellä arvioita todelliselle arvolle, mikä avaisi monia mahdollisuuksia matematiikan eri aloilla. on olemassa monia tärkeitä hypoteeseja, joiden mukaan ”Jos Riemannin hypoteesi on totta, niin …”, niin tämän ongelman ratkaiseminen vahvistaisi välittömästi myös kaikki seuraavat oletukset.