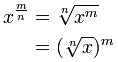Kutsutaan myös ”radikaaleiksi” tai ”järkeviksi eksponenteiksi”
kokonaislukueksponentit
Tarkastellaan ensin kokonaislukua eksponentit:

Numeron eksponentti kertoo kuinka monta kertaa numeroa tulee käyttää kertolaskussa.
Tässä esimerkissä: 82 = 8 × 8 = 64
Toinen esimerkki: 53 = 5 × 5 × 5 = 125
Murtolukueksponentit
Mutta entä jos eksponentti on murtoluku?
>
14-asteen eksponentti on 4. juuri
Ja niin edelleen!

Miksi?
Katsotaan ”s” miksi esimerkki.
Ensinnäkin eksponenttien lait kertoivat meille, kuinka eksponentteja käsitellään, kun kerrotaan:
Esimerkki: x2x2 = (xx) (xx) = xxxx = x4
Mikä osoittaa, että x2x2 = x (2 + 2) = x4
Kokeile siis murtolukujen kanssa:
Kokeile toista osaa
Yritetään sitä uudelleen, mutta neljänneksen (1/4) asteikolla:
Esimerkki:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Joten 4 kertaa kerrannaisena käytetty 16¼ antaa arvon 16,
ja niin 16¼ on 16: n 4. juuret
Yleissääntö
Se toimi ½: n kanssa, se toimi with: n kanssa, itse asiassa se toimii yleensä:
x1 / n = X: n n: n juuri
Joten voimme keksiä tämän:
| |
|
Esimerkki: Mikä on 271/3?
Vastaus: 271/3 = ![]() 27 = 3
27 = 3
Entä monimutkaisemmat jakeet?
Entä murtoluku, kuten 43/2?
Se tarkoittaa todella kuution (3) ja neliöjuuren (1/2) tekemistä missä tahansa järjestyksessä.
Haluan selittää.
Murtoluku (kuten m / n) voidaan jakaa kahteen osaan:
- kokonaislukuosa (m) ja
- murtoluku (1 / n) osa
Joten, koska m / n = m × (1 / n), voimme tehdä tämän:
Järjestyksellä ei ole merkitystä, joten se toimii myös m / n = (1 / n) × m: lle:
Ja saamme tämän:
| |
|
Joitakin esimerkkejä:
Esimerkki : Mikä on 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
tai
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
Kummallakin tavalla saadaan sama tulos.
Esimerkki: Mikä on 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
tai
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
Se oli varmasti helpompi toinen tapa!
Nyt … Pelaa grafiikalla!
Katso kuinka sujuvasti käyrä muuttuu, kun pelaat murtoluvuilla tämä animaatio osoittaa, että tämä murto-osien eksponenttien idea sopii yhteen kauniisti:
Kokeilemisen varaa:
- Aloita m = 1 ja n = 1, lisää sitten hitaasti n niin, että näet 1/2, 1/3 ja 1/4
- Kokeile sitten m = 2 ja liu’uttamalla n ylös ja alas nähdäksesi murtoluvut, kuten 2/3 jne.
- Yritä nyt tehdä eksponentista -1
- Yritä lopuksi lisätä m, pienentää sitten n, pienentää sitten m ja lisätä sitten n: käyrän tulisi kulkea ympäri ja sen ympäri