Mikä on keskihajonta? | STDEV.P | STDEV.S | Varianssi
Tällä sivulla selitetään, kuinka lasketaan keskihajonta koko populaation perusteella käyttämällä Excelin STDEV.P-funktiota ja kuinka arvioida keskihajonta otoksen perusteella käyttämällä Excelin STDEV.S-funktiota.
Mikä on keskihajonta?
Keskihajonta on luku, joka kertoo kuinka kaukana luvut ovat keskiarvostaan.
1. Esimerkiksi alla olevien numeroiden keskiarvo (keskiarvo) on 10.
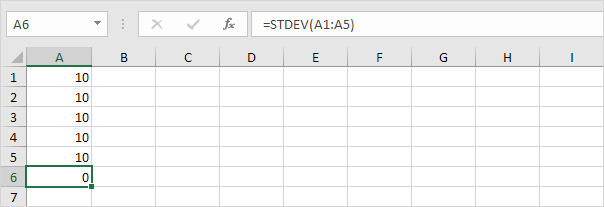
Selitys: numerot ovat kaikki samat, jotka tarkoittaa, että vaihtelua ei ole. Tämän seurauksena numeroiden keskihajonta on nolla. STDEV-funktio on vanha funktio. Microsoft Excel suosittelee uuden STEDV.S-funktion käyttöä, joka tuottaa täsmälleen saman tuloksen.
2. Alla olevien numeroiden keskiarvo (keskiarvo) on myös 10.
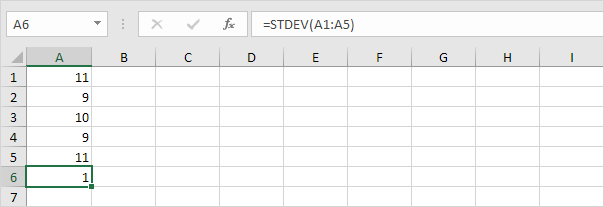
Selitys: luvut ovat lähellä keskiarvoa. Tämän seurauksena numeroiden keskihajonta on pieni.
3. Alla olevien numeroiden keskiarvo (keskiarvo) on myös 10.
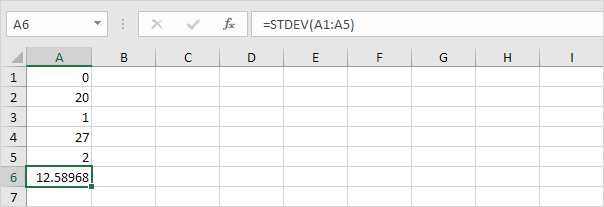
Selitys: numerot ovat hajautettuja. Tämän seurauksena numeroilla on suuri keskihajonta.
STDEV.P
Excelin STDEV.P-funktio (P tarkoittaa väestöä) laskee keskihajonnan koko populaation perusteella. Esimerkiksi opetat 5 opiskelijan ryhmää. Sinulla on kaikkien opiskelijoiden testitulokset. Koko populaatio koostuu viidestä datapisteestä. STDEV.P-funktio käyttää seuraavaa kaavaa:
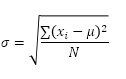
Tässä esimerkissä x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (keskiarvo), N = 5 (datapisteiden lukumäärä).
1. Laske keskiarvo (μ).
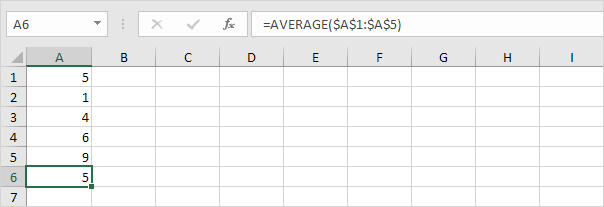
2. Laske kullekin numerolle etäisyys keskiarvoon.
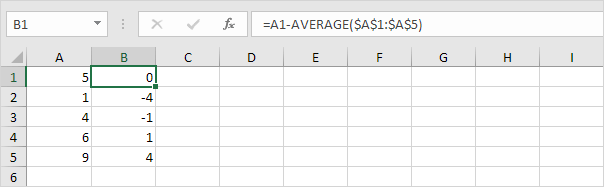
3. Neliö tämä etäisyys jokaiselle numerolle.
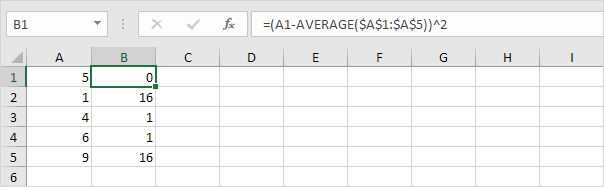
4. Summa (∑) nämä arvot.
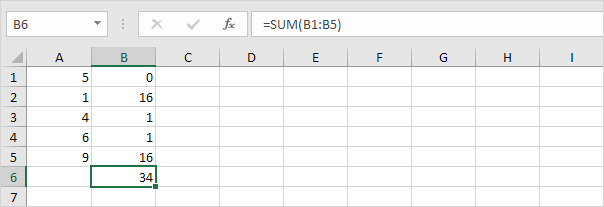
5. Jaa datapisteiden lukumäärällä (N = 5).
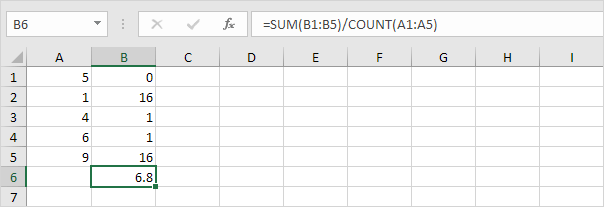
6. Ota neliöjuuri.
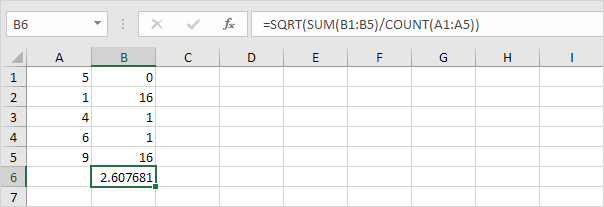
7. Onneksi Excelin STDEV.P-toiminto voi suorittaa kaikki nämä vaiheet puolestasi.
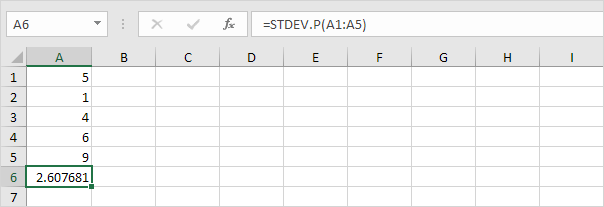
STDEV.S
STDEV.S-funktio (S tarkoittaa Sample) Excelissä arvioi keskihajonnan otoksen perusteella. Esimerkiksi opetat suurta joukkoa opiskelijoita. Testituloksia on vain 5 opiskelijaa. Otoksen koko on 5. STDEV.S-funktiossa käytetään seuraavaa kaavaa:
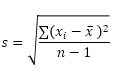
Tässä esimerkissä x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (samat numerot kuin yllä), x̄ = 5 (näyte keskiarvo), n = 5 (otoksen koko).
1. Toista yllä olevat vaiheet 1–5, mutta jaa vaiheessa 5 n-1: llä N.: n sijasta.
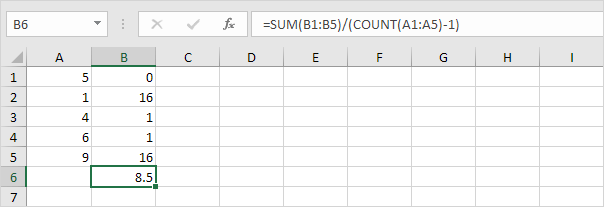
2. Ota neliöjuuri.
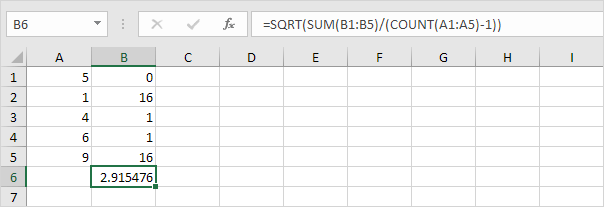
3. Onneksi Excelin STDEV.S-toiminto voi suorittaa kaikki nämä vaiheet puolestasi.
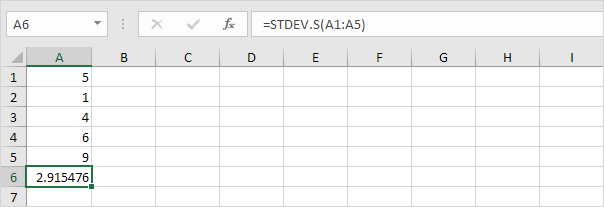
Huomaa: miksi jaamme n – 1 n: n sijasta, kun arvioimme keskihajonnan otoksen perusteella? Besselin korjaus toteaa, että jakamalla n-1: llä n: n sijasta saadaan parempi arvio keskihajonnasta.
Varianssi
Varianssi on keskihajonnan neliö. Se on niin yksinkertaista. Joskus on varianssin käyttäminen helpompaa tilastollisten ongelmien ratkaisemisessa.
1. Alla oleva VAR.P-funktio laskee varianssin koko populaation perusteella.
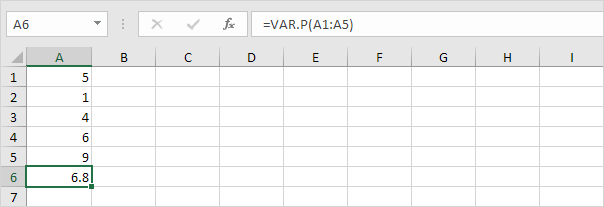
Huomaa: tiesit jo tämän vastauksen (katso vaihe 5 kohdassa STDEV.P). Ota tämän tuloksen neliöjuuri löytääksesi koko populaatioon perustuvan keskihajonnan.
2. Alla oleva VAR.S-toiminto arvioi varianssin näytteen perusteella.
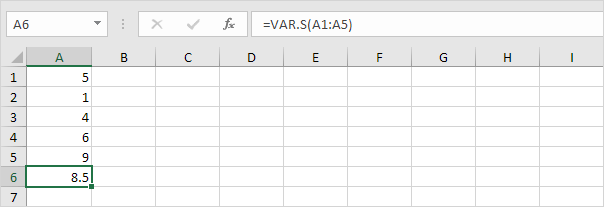
Huomaa: tiesit jo tämän vastauksen (katso vaihe 1 kohdassa STDEV.S). Ota tämän tuloksen neliöjuuri löytääksesi standardipoikkeaman näytteen perusteella.
3. VAR ja VAR.S tuottavat täsmälleen saman tuloksen.
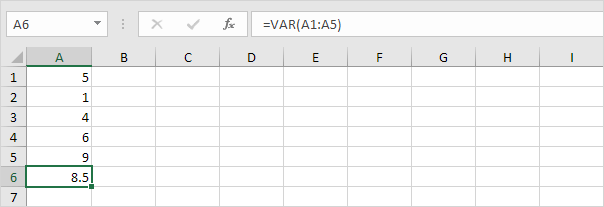
Huomaa: Microsoft Excel suosittelee uuden VAR.S-toiminnon käyttöä.