標準偏差とは何ですか? | STDEV.P | STDEV.S |分散
このページでは、ExcelのSTDEV.P関数を使用して母集団全体に基づいて標準偏差を計算する方法と、ExcelのSTDEV.S関数を使用してサンプルに基づいて標準偏差を推定する方法について説明します。
標準偏差とは何ですか?
標準偏差は、数値が平均からどれだけ離れているかを示す数値です。
1。たとえば、以下の数値の平均(平均)は10です。
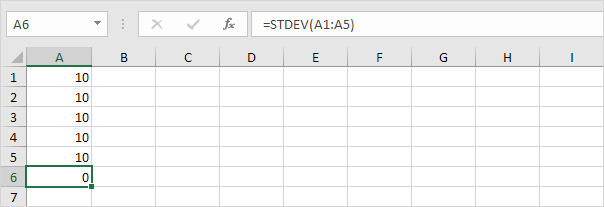
説明:数値はすべて同じで、変動がないことを意味します。その結果、数値の標準偏差はゼロになります。STDEV関数は古い関数です。MicrosoftExcelでは、まったく同じ結果を生成する新しいSTEDV.S関数を使用することをお勧めします。
2.以下の数値の平均(平均)も10です。
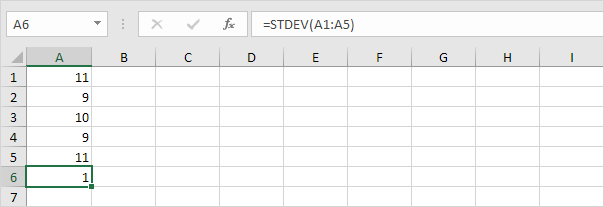
説明:数値は平均に近いため、標準偏差が低くなっています。
3.以下の数値の平均(平均)も10です。
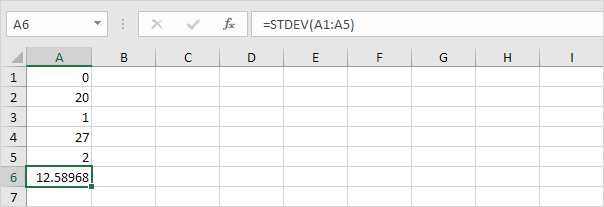
説明:数値が分散しているため、数値の標準偏差が高くなっています。
STDEV.P
ExcelのSTDEV.P関数(PはPopulationを表す)は、母集団全体に基づいて標準偏差を計算します。たとえば、5人の学生のグループを教えています。あなたはすべての学生のテストスコアを持っています。母集団全体は5つのデータポイントで構成されています。 STDEV.P関数は、次の式を使用します。
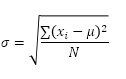
この例では、x1 = 5、x2 = 1、x3 = 4、x4 = 6、x5 = 9、μ= 5(平均)、N = 5(データポイントの数)。
1。平均(μ)を計算します。
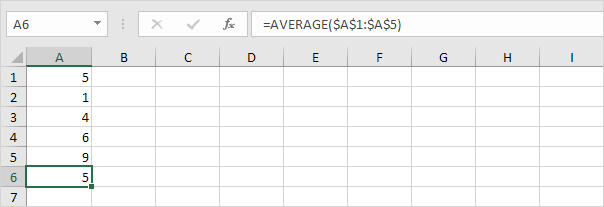
2。数値ごとに、平均までの距離を計算します。
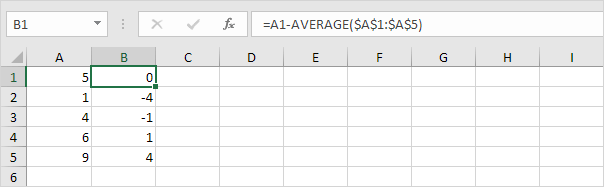
3。数値ごとに、この距離を2乗します。
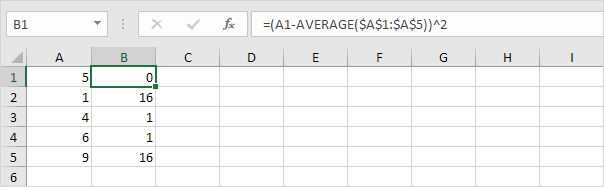
4。これらの値を合計(∑)します。
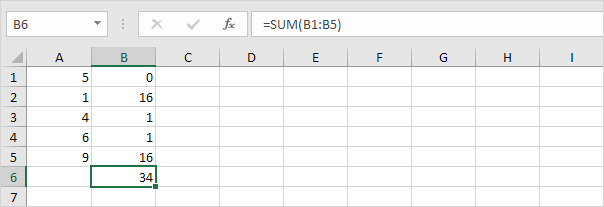
5。データポイントの数で割ります(N = 5)。
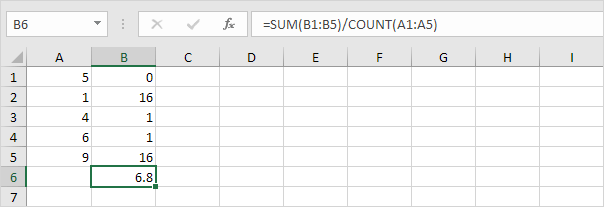
6。平方根を取ります。
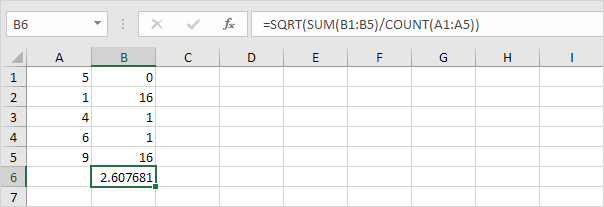
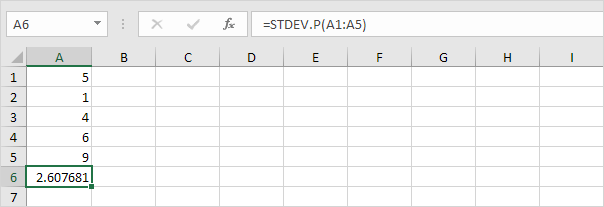
7。幸い、ExcelのSTDEV.P関数を使用すると、これらすべての手順を実行できます。
STDEV.S
ExcelのSTDEV.S関数(Sはサンプルを表す)は、サンプルに基づいて標準偏差を推定します。たとえば、「大勢の学生を教えています。テストスコアは5人しかありません。サンプルサイズは5です。STDEV.S関数は次の式を使用します。
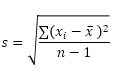
この例では、x1 = 5、x2 = 1、x3 = 4、x4 = 6、x5 = 9(上記と同じ番号)、x̄= 5(サンプル平均)、n = 5(サンプルサイズ)。
1。上記の手順1〜5を繰り返しますが、手順5でNではなくn-1で除算します。
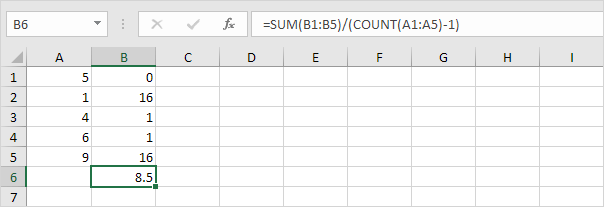
2。平方根を取ります。
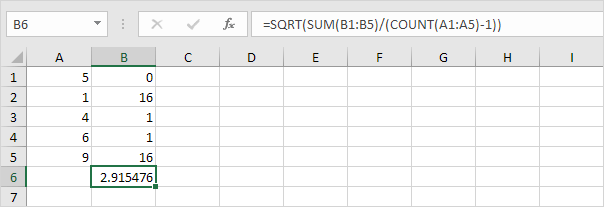
3。幸い、ExcelのSTDEV.S関数を使用すると、これらすべての手順を実行できます。
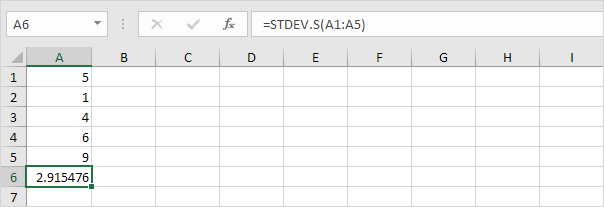
注:なぜ除算するのですか?サンプルに基づいて標準偏差を推定する場合、nではなくn-1?ベッセルの修正では、nではなくn-1で除算すると、標準偏差の推定が向上すると述べています。
分散
差異は、標準偏差の2乗です。とても簡単です。統計的な問題を解くときに分散を使用する方が簡単な場合があります。
1。以下のVAR.P関数は、母集団全体に基づいて分散を計算します。
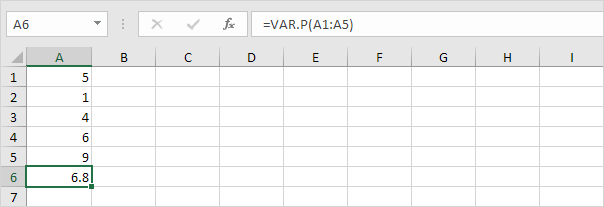
注:この回答はすでに知っています(を参照)。 STDEV.Pのステップ5)。この結果の平方根を取り、母集団全体に基づいた標準偏差を見つけます。
2。以下のVAR.S関数は、サンプルに基づいて分散を推定します。
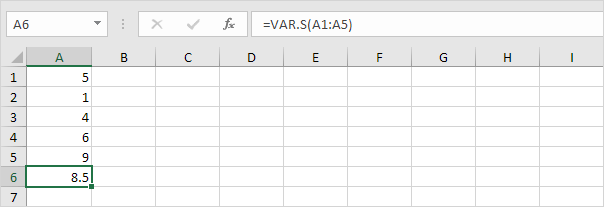
注:この回答はすでに知っています(手順を参照)。 STDEV.Sの下で1)。この結果の平方根を取り、サンプルに基づいて標準偏差を見つけます。
3。 VARとVAR.Sはまったく同じ結果を生成します。
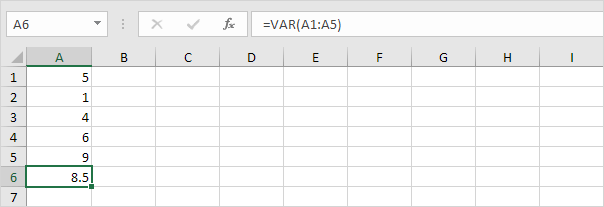
注:Microsoft Excelでは、新しいVAR.S関数を使用することをお勧めします。