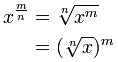「ラジカル」または「合理的な指数」とも呼ばれます
整数の指数
まず、整数を見てみましょう。指数：
数値の指数は、数値を使用する回数を示します乗算で。
この例では：82 = 8×8 = 64
別の例：53 = 5×5×5 = 125
分数の指数
しかし、指数が分数の場合はどうでしょうか。
|
12の指数は実際には平方根です 13の指数は立方根です 14の指数は4乗根です などです！ |
 |
理由
理由を例。
最初に、指数の法則は、乗算するときに指数を処理する方法を示しています。
例：x2x2 =（xx）（xx）= xxxx = x4
これは、x2x2 = x（2 + 2）= x4
それを分数の指数で試してみましょう：
別の分数を試してください
もう一度試してみましょう。ただし、指数は1/4（1/4）です。
例：
16¼×16¼×16¼ ×16¼= 16（¼+¼+¼+¼）= 16（1）= 16
したがって、16¼を乗算で4回使用すると、16が得られます
したがって、16¼は16の4乗根
一般規則
½で機能し、¼で機能しました。実際、一般的に機能します：
x1 / n = xのn番目のルート
これを思い付くことができます：
 |
|
例：271/3とは何ですか？
回答：271/3 = 
27 = 3
より複雑な分数についてはどうですか？
43/2のような分数指数についてはどうですか？
つまり、立方体（3）と平方根（1/2）を任意の順序で実行するということです。
説明させてください。
分数（m / nなど）は2つの部分に分けることができます：
- 整数部分（m）と
- 分数（1 / n）部分
つまり、m / n = m×（1 / n）なので、次のことができます。
順序は重要ではないので、 m / n =（1 / n）×mでも機能します：
次のようになります：
| |
|
いくつかの例：
例：43/2とは何ですか？
43/2 = 43×（1/2）=√（43）=√（4×4×4）=√（64）= 8
または
43/2 = 4（1/2）×3 =（√4）3 =（2）3 = 8
どちらの方法でも同じ結果が得られます。
例：274/3とは何ですか？
274 / 3 = 274×（1/3）= （274）= （531441）= 81
または
274/3 = 27（1/3）×4 =（ 27）4 =（3）4 = 81
2番目の方法は確かに簡単でした！
今…グラフで遊んでください！
で分数を使って遊ぶと、曲線がどれほどスムーズに変化するかを確認してくださいこのアニメーションは、この分数指数の考え方がうまく調和していることを示しています。
試してみる：
- m = 1とn = 1から始めて、ゆっくりと増やしていきます。 n 1 / 2、1 / 3、1 / 4が見えるようにします
- 次に、m = 2を試し、nを上下にスライドして、2/3などの分数を確認します
- 次に、指数を-1にしようとします。
- 最後に、mを増やし、次にnを減らし、次にmを減らし、次にnを増やします。曲線はぐるぐる回るはずです