ポアンカレ予想と他の6つの複雑な数学理論は、クレイ数学研究所(CMI)によってミレニアム懸賞問題と呼ばれています。それぞれの問題は「長年にわたって解決策に抵抗してきた重要な古典的な質問」として説明されており、CMIの好意でそれぞれが$ 1,000,000を稼ぐための解決策を最初に考案しました。ただし、上記のように、これらの問題を解決するのは簡単ではありません。 feat。1859年にドイツの数学者ベルンハルトリーマンによって定式化されて以来、問題の1つは未解決のままです。
前述のドイツの数学者にちなんで名付けられたリーマン予想は、純粋で最も重要な未解決の問題であると広く考えられています。数学:生物学から暗号化、量子力学まであらゆる分野で使用される素数の分布に関する結果を意味するため、数論に大きな関心が寄せられています。リーマン予想を理解するには、まずいくつかの重要な点を説明する必要があります。概念:
- 複素数はa + biの形式で、iはi²= -1で定義されます。この形式では、複素数の実数部はaであり、虚数はaです。一部はbiです。
- リーマンゼータ関数は、次の式で定義される複素変数(複素数の関数)の関数です。ここで、sは1以外の任意の複素数であり、その値も複素数です。
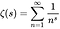
- 関数の「ゼロ」は、f(x)のようなxです。 = 0
- リーマンゼータ関数の「自明な零点」はすべて負の偶数の整数(-2、-4、-6、…)
- 「自明でない零点」リーマンゼータ関数の」は、ζ(s)= 0であるsの他のすべての値です(つまり、 sは負の偶数の整数ではありません。
これでいくつかの定義ができたので、リーマン予想を述べることができます。
リーマンゼータ関数のすべての自明でないゼロの実数部は1/2です
これは(私にとって)少なくとも)ポアンカレ予想よりもはるかに理解しやすく、直感的にはそれほど難しいようには見えません。しかし、それもあまり意味がないようです。本当に、このランダム関数の値が0のときは誰が気にしますか。当然のことながら、多くの数学者はそうしますが、非常に理由があります。
一部の数値には、表現できないという特別な特性があります。 2つの小さい数の積(積は乗算)として、すなわち。 2、3、5、7、11など。素数として知られているこれらは、ある意味で最も単純な数であり、他のすべての数の構成要素を形成します。しかし、イライラすることに、素数はどのパターンにも従わないようです。 3137は素数であり、その後の次の数は3163までではありませんが、3167と3169がすばやく連続して続き、すべてが素数です。一言で言えば、1つの素数を見つけた場合、すべての素数を確認せずに、次の素数がどこにあるかを知る方法はありません。ただし、素数定理(PNT)を使用すると、特定のしきい値を下回る素数の数を見つけることができます。
素数定理は単なる推定値であり、値が異なると、存在する確率も異なります。正しいですが、100%確実ではありません。ただし、リーマン予想が真であるという仮定を理解すると、素数定理とリーマンゼータ関数の自明でないゼロを組み合わせた数学的近似を作成して、内部コンポーネントをエラー修正し、次の「可能な限り最良の」境界を提供できます。素数定理の誤差項。リーマン予想を完全に証明できれば、PNTは実際の値に非常に近い推定値を提供できるようになり、数学のさまざまな分野で多くの可能性が開かれます。 「リーマン予想が真なら…」という重要な仮説がたくさんあるので、この問題を解くと、その後のすべての推測も即座に検証されます。