표준 편차 란 무엇입니까? | STDEV.P | STDEV.S | 분산
이 페이지에서는 Excel의 STDEV.P 함수를 사용하여 전체 모집단을 기준으로 표준 편차를 계산하는 방법과 Excel의 STDEV.S 함수를 사용하여 표본을 기반으로 표준 편차를 추정하는 방법을 설명합니다.
표준 편차 란 무엇입니까?
표준 편차는 숫자가 평균에서 얼마나 멀리 떨어져 있는지 알려주는 숫자입니다.
1. 예를 들어 아래 숫자의 평균 (평균)은 10입니다.
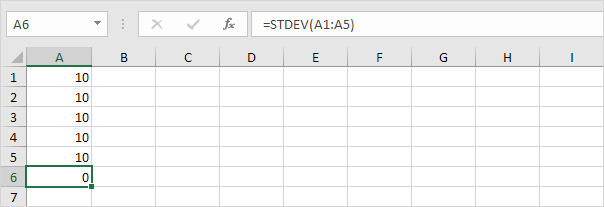
설명 : 숫자는 모두 동일합니다. 변화가 없음을 의미합니다. 결과적으로 숫자의 표준 편차가 0입니다. STDEV 함수는 이전 함수입니다. Microsoft Excel에서는 정확히 동일한 결과를 생성하는 새로운 STEDV.S 함수를 사용할 것을 권장합니다.
2. 아래 숫자의 평균 (평균)도 10입니다.
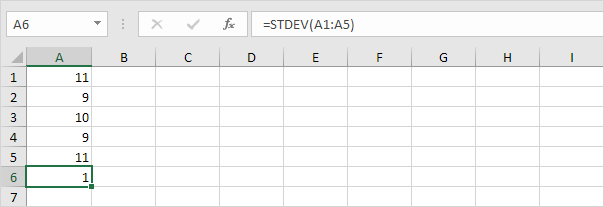
설명 : 숫자가 평균에 가까워서 표준 편차가 낮습니다.
3. 아래 숫자도 평균 (평균) 10입니다.
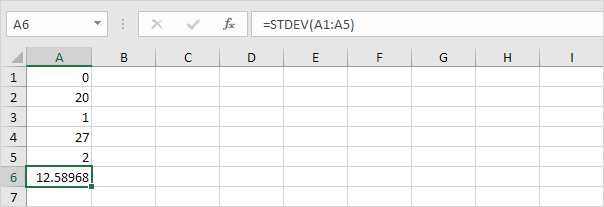
설명 : 숫자가 분산되어 있으므로 숫자의 표준 편차가 높습니다.
STDEV.P
Excel의 STDEV.P 함수 (P는 인구를 나타냄)는 전체 모집단을 기준으로 표준 편차를 계산합니다. 예를 들어 5 명의 학생 그룹을 가르치고 있습니다. 모든 학생의 시험 점수가 있습니다. 전체 모집단은 5 개의 데이터 포인트로 구성됩니다. STDEV.P 함수는 다음 공식을 사용합니다.
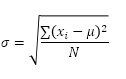
이 예에서 x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (평균), N = 5 (데이터 포인트 수)
1. 평균 (μ)을 계산합니다.
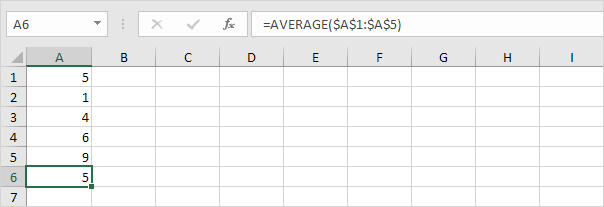
2. 각 숫자에 대해 평균까지의 거리를 계산합니다.
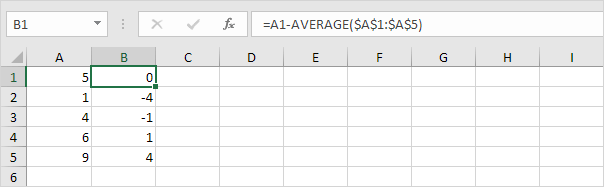
3. 각 숫자에 대해이 거리를 제곱합니다.
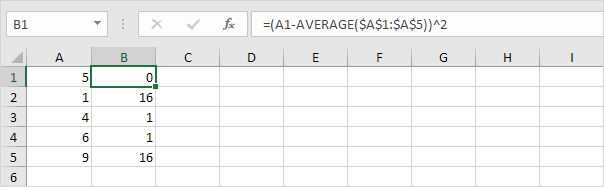
4. 이 값을 더합니다 (∑).
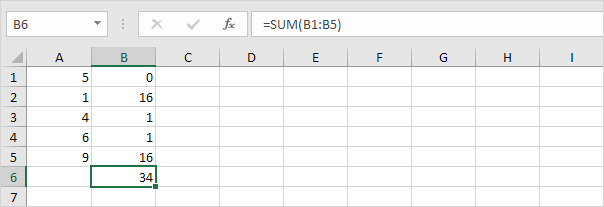
5. 데이터 포인트 수로 나눕니다 (N = 5).
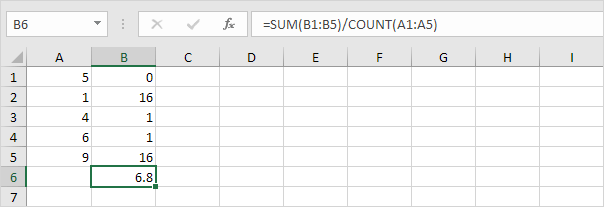
6. 제곱근을 취합니다.
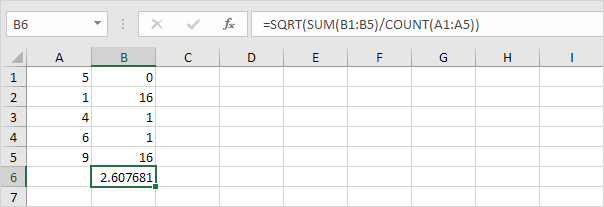
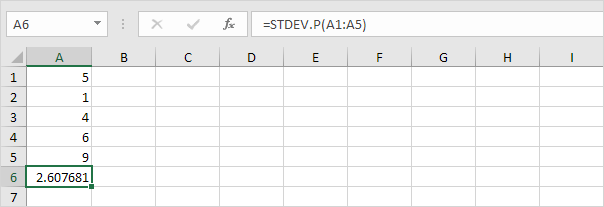
7. 다행히 Excel의 STDEV.P 함수는 이러한 모든 단계를 대신 실행할 수 있습니다.
STDEV.S
Excel의 STDEV.S 함수 (S는 샘플을 나타냄)는 샘플을 기반으로 표준 편차를 추정합니다. 예를 들어 “대규모 학생 그룹을 가르치고 있습니다. 학생 5 명의 시험 점수 만 있습니다. 샘플 크기는 5입니다. STDEV.S 함수는 다음 공식을 사용합니다.
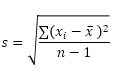
이 예에서는 x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (위와 같은 숫자), x̄ = 5 (샘플 평균), n = 5 (샘플 크기).
1. 위의 1-5 단계를 반복하되 5 단계에서는 N 대신 n-1로 나눕니다.
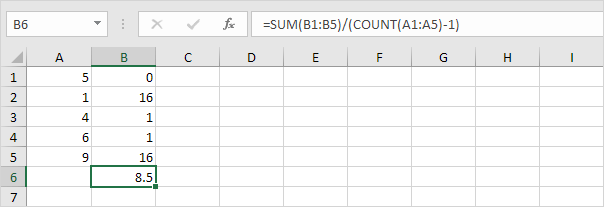
2. 제곱근을 취합니다.
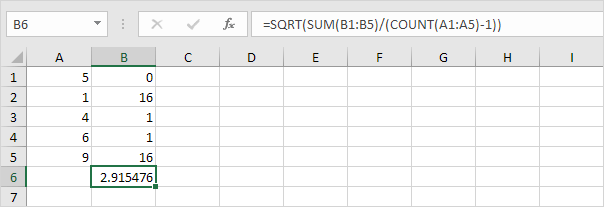
3. 다행히 Excel의 STDEV.S 함수는이 모든 단계를 수행 할 수 있습니다.
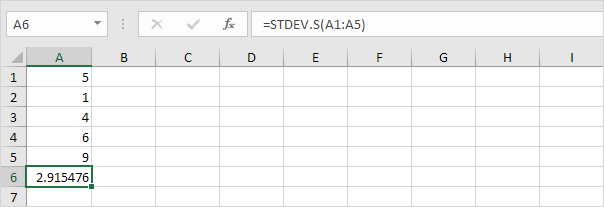
참고 : 표본을 기반으로 표준 편차를 추정 할 때 n 대신 n-1? Bessel의 수정에 따르면 n 대신 n-1로 나누면 표준 편차를 더 잘 추정 할 수 있습니다.
분산
분산은 표준 편차의 제곱입니다. 간단합니다. 때로는 통계 문제를 해결할 때 분산을 사용하는 것이 더 쉽습니다.
1. 아래의 VAR.P 함수는 전체 모집단을 기준으로 분산을 계산합니다.
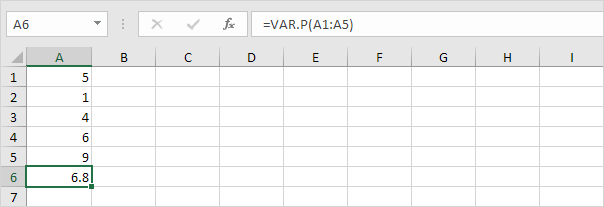
참고 : 이미이 답변을 알고 계십니다 ( STDEV.P의 5 단계). 전체 모집단을 기준으로 표준 편차를 구하려면이 결과의 제곱근을 구하십시오.
2. 아래 VAR.S 함수는 샘플을 기반으로 분산을 추정합니다.
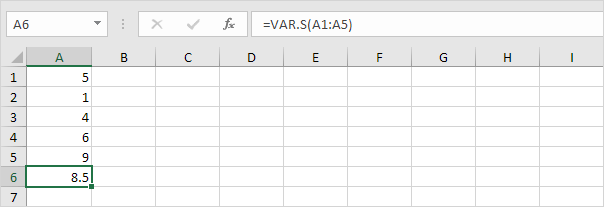
참고 : 이미이 답변을 알고 계십니다 (단계 참조). STDEV.S에서 1). 이 결과의 제곱근을 취하여 표본을 기반으로 한 표준 편차를 찾습니다.
3. VAR 및 VAR.S는 정확히 동일한 결과를 생성합니다.
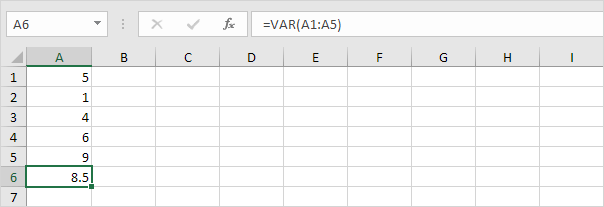
참고 : Microsoft Excel에서는 새 VAR.S 함수를 사용할 것을 권장합니다.