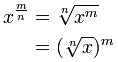“Radicals”또는 “Rational Exponents”라고도 함
정수 지수
먼저 정수를 살펴 보겠습니다. 지수 :
숫자의 지수는 숫자를 사용하는 횟수를 나타냅니다. 곱셈으로.
이 예에서 : 82 = 8 × 8 = 64
다른 예 : 53 = 5 × 5 × 5 = 125
분수 지수
하지만 지수가 분수라면 어떨까요?
|
12의 지수는 실제로 제곱근입니다. 13의 지수는 세제곱근입니다. 14의 지수는 4 근 등입니다! |
 |
이유
예.
먼저, 지수의 법칙은 곱할 때 지수를 처리하는 방법을 알려줍니다.
예 : x2x2 = (xx) (xx) = xxxx = x4
x2x2 = x (2 + 2) = x4
그러므로 분수 지수로 시도해 보겠습니다.
다른 분수 시도
다시 시도해 보겠습니다. 그러나 지수는 1/4 (1/4)입니다.
예 :
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
따라서 16¼을 곱셈에서 4 번 사용하면 16이됩니다.
16의 네 번째 루트
일반 규칙
½에서 작동했고 ¼에서 작동했습니다. 실제로 일반적으로 작동합니다.
x1 / n = x의 n 번째 루트
그러면 다음과 같은 결과를 얻을 수 있습니다.
 |
|
예 : 271/3은 무엇입니까?
답변 : 271/3 = 
27 = 3
더 복잡한 분수는 어떻습니까?
43/2와 같은 분수 지수는 어떻습니까?
정육면체 (3)와 제곱근 (1/2)을 순서에 관계없이 수행하는 것입니다.
설명하겠습니다.
분수 (예 : m / n)는 두 부분으로 나눌 수 있습니다.
- 정수 부분 (m) 및
- 분수 (1 / n) 부분
그러므로 m / n = m × (1 / n)이므로 다음과 같이 할 수 있습니다.
순서는 중요하지 않습니다. m / n = (1 / n) × m에서도 작동합니다 :
그리고 우리는 이것을 얻습니다 :
| |
|
예 :
예 : 43/2는 무엇입니까?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
또는
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
어느 쪽이든 동일한 결과를 얻습니다.
예 : 274/3은 무엇입니까?
274 / 3 = 274 × (1/3) = (274) = (531441) = 81
또는
274/3 = 27 (1/3) × 4 = ( 27) 4 = (3) 4 = 81
두 번째 방법은 확실히 더 쉬웠습니다!
그래프를 가지고 놀아요!
분수를 가지고 놀 때 곡선이 얼마나 매끄럽게 변하는 지 확인하세요. 이 애니메이션은 분수 지수에 대한 아이디어가 잘 어울리는 것을 보여줍니다.
시도 할 사항 :
- m = 1 및 n = 1로 시작한 다음 천천히 증가 n 1/2, 1/3 및 1/4을 볼 수 있도록
- 그런 다음 m = 2를 시도하고 n을 위아래로 슬라이드하여 2/3 등의 분수를 확인
- 이제 지수를 -1로 만드세요
- 마지막으로 m을 늘린 다음 n을 줄인 다음 m을 줄인 다음 n을 늘립니다. 곡선이 돌아서야합니다.