Poincaré Conjecture 및 6 개의 다른 복잡한 수학적 이론은 Clay Mathematics Institute (CMI)에서 Millennium Prize Problems라고 불렀습니다. 각 문제는 “수년에 걸쳐 해결책에 저항해온 중요한 고전적인 질문”으로 설명되어 있으며, 각 문제에 대한 해결책을 최초로 고안 한 사람은 CMI로부터 $ 1,000,000를 받았습니다. 그러나 위에서 본 것처럼 이러한 문제를 해결하는 것은 쉽지 않습니다. feat. 독일 수학자 Bernhard Riemann이 1859 년에 공식화 한 이후 문제 중 하나가 해결되지 않았습니다.
앞서 언급 한 독일 수학자의 이름을 딴 Riemann Hypothesis는 순수에서 가장 중요한 미해결 문제로 널리 간주됩니다. 수학입니다. 생물학에서 암호화 및 양자 역학에 이르기까지 모든 분야에서 사용되는 소수 분포에 대한 결과를 암시하기 때문에 수 이론에 큰 관심이 있습니다. 리만 가설을 이해하기 위해 먼저 몇 가지 핵심 사항을 설명해야합니다. 개념 :
- 복소수는 a + bi 형식입니다. 여기서 i는 i² = -1로 정의됩니다.이 형식에서 복소수의 실수 부분은 a이고 허수는 부분은 bi입니다.
- Riemann zeta 함수는 다음 방정식으로 정의 된 복소수 (복소수의 함수)의 함수입니다. 여기서 s는 1이 아닌 복소수이고 값도 복소수입니다.
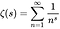
- 함수의 “0”은 f (x)가되는 x입니다. = 0
- Riemann zeta 함수의 “사소한 0″은 모두 음의 짝수 (-2, -4, -6,…)입니다.
- “사소하지 않은 0” Riemann zeta 함수의”는 ζ (s) = 0 (즉. s는 음의 짝수가 아닙니다).
이제 몇 가지 정의가 내려 졌으므로 계속해서 리만 가설을 말할 수 있습니다.
리만 제타 함수의 모든 중요하지 않은 0의 실제 부분은 1/2입니다.
적어도)는 Poincaré 추측보다 이해하기 훨씬 쉬우 며 직관적으로 그리 어렵지 않은 것 같습니다. 그러나 그것은 또한 그다지 의미가없는 것 같습니다. 이 임의의 함수가 0의 값을 가질 때 누가 신경을 써야할까요. 당연히 많은 수학자들이 그렇게합니다. 아주 좋은 이유가 있습니다.
어떤 숫자는 표현할 수없는 특별한 속성을 가지고 있습니다. 두 개의 작은 숫자의 곱 (곱은 곱임), 즉. 2,3,5,7,11 등. 소수로 알려진이 숫자는 어떤 의미에서 얻을 수있는 가장 단순한 숫자이며 다른 모든 숫자의 구성 요소를 형성합니다. 그러나 실망스럽게도 소수는 어떤 패턴도 따르지 않는 것 같습니다. 3137은 소수이고 그 다음 숫자는 3163까지는 아니지만 3167과 3169가 빠르게 연속적으로 이어지며 모두 소수입니다. 간단히 말해서, 소수 하나를 찾으면 모든 숫자를 확인하지 않고는 다음 숫자가 어디에 있을지 알 수있는 방법이 없습니다. 그러나 소수 정리 (PNT)를 사용하면 특정 임계 값 아래에 소수가 몇 개 있는지 확인할 수 있습니다.
소수 정리는 다른 값을 사용하여 존재 확률이 다른 추정치입니다. 정확하지만 절대 100 % 확실하지 않습니다. 그러나 Reimann 가설이 참이라는 가정을 이해하면 Prime Number Theorem과 Riemann zeta 함수의 사소하지 않은 0을 결합하여 수학적 근사를 생성하여 내부 구성 요소를 오류 수정하여 “최상의”한계를 제공 할 수 있습니다. Reimann Hypothesis를 완전히 증명할 수 있다면, 이것은 PNT가 실제 값에 엄청나게 근접한 추정치를 제공 할 수있는 능력을 제공하여 다양한 수학 분야에서 많은 가능성을 열어 줄 것입니다. “리만 가설이 사실이라면…”이라는 중요한 가설이 많이 있으므로이 문제를 해결하면 모든 후속 추측도 즉시 검증됩니다.