Kosten-Volumen-Gewinn-Analyse

Die Kosten-Volumen-Gewinn-Analyse (CVP) ist eine betriebliche Buchhaltungstechnik, mit der die Auswirkungen des Umsatzvolumens und der Produktkosten auf das Betriebsergebnis eines Unternehmens untersucht werden. Es zeigt, wie sich Änderungen der variablen Kosten, der Fixkosten, des Verkaufspreises pro Einheit und des Verkaufsmix von zwei oder mehr Produkten auf das Betriebsergebnis auswirken. Die CVP-Analyse befasst sich mit der Ermittlung der Fixkosten eines Unternehmens , seine variablen Kosten pro Einheit, den Preis seines Produkts und die Verwendung dieser Daten, um die folgenden Maßnahmen zu ermitteln:

• Deckungsbeitrag: Die Differenz zwischen dem Gesamtumsatz eines Unternehmens und den gesamten variablen Kosten. Dies ist der Betrag, den der Umsatz zu Fixkosten und Gewinn beiträgt.
• Deckungsbeitrag pro Einheit: Die Differenz zwischen Verkaufspreis und variablen Kosten pro Einheit.
• Deckungsbeitragsverhältnis: Das Verhältnis von Deckungsbeitrag zum Gesamtumsatz.
• Break-Even-Punkt: Das Verkaufsvolumen (in Einheiten und Dollar), bei dem das Unternehmen weder Verluste macht noch Gewinne erzielt.
• Zieleinkommensverkäufe: Das erforderliche Umsatzniveau
• Sicherheitsspanne: Der Prozentsatz (oder die Dollars), um den das Umsatzvolumen eines Unternehmens seinen Break-Even-Punkt überschreitet.

Die Der kritischste Input bei der CVP-Analyse ist die Beziehung zwischen verschiedenen Kosten und Volumen, dh die Kategorisierung der Kosten in feste und variable Kategorien.

CVP-Analysegleichung

Die grundlegende Kosten-Volumen-Gewinn-Beziehung kann aus der Gewinngleichung abgeleitet werden:

Gewinn = Umsatz – Fixkosten – Variable Kosten

Wenn Gewinn PR ist, entspricht der Umsatz dem Produkt aus Preis pro Einheit P und Verkaufsvolumen in Einheiten Q. , Fixkosten FC sind konstant und die variablen Gesamtkosten entsprechen dem Produkt der verkauften Einheiten Q und den variablen Kosten pro Einheit V. Die folgende Gleichung ist eine detailliertere Darstellung der CVP-Beziehungen:

PR = Q × P – Q × V – FC

Dies ist die grundlegendste Gleichung, mit der viele CVP-Zahlen bearbeitet werden können.

Für Unterbrechungen – Auch wenn wir PR ad 0 setzen und nach Q auflösen müssen, erhalten wir:

Break-Even Q = FC ÷ (P – V)

Es zeigt, dass break- Ein gerader Punkt kann berechnet werden, indem die Fixkosten durch den Deckungsbeitrag pro Einheit dividiert werden.

Ansatz der Deckungsbeitragsgleichung

Die oben diskutierte CVP-Gleichung kann auch als Deckungsbeitrag des ausgedrückt werden Produkt:

PR = Q × P – Q × V – FC

PR = Q × (P – V) – FC

(P – V) In der obigen Gleichung ist der Deckungsbeitrag pro Einheit angegeben.

CVP-Diagramm

Die CVP-Beziehung kann auch in Form eines Diagramms mit dem Namen CVP-Diagramm ausgedrückt werden:

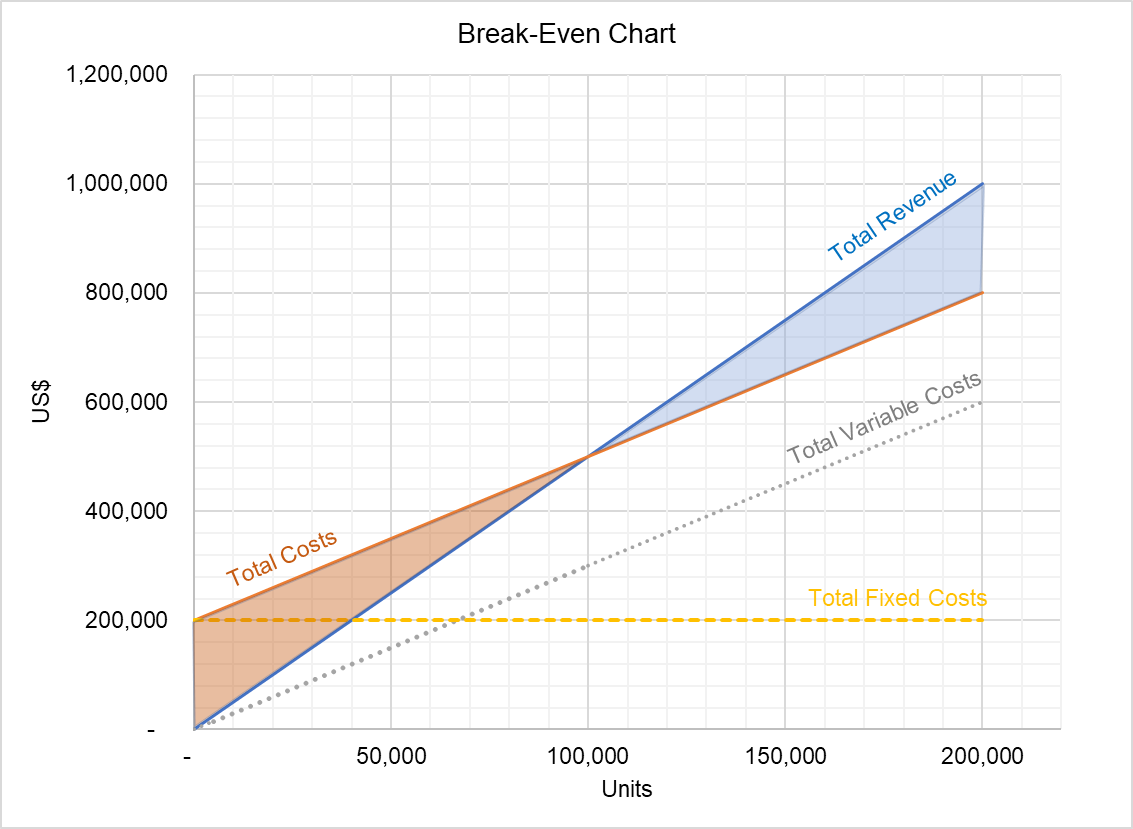
Die obige Grafik zeigt die Beziehung zwischen Gesamtumsatz und Gesamtkosten. Der Bereich zwischen den beiden Linien unterhalb des Break-Even-Punkts stellt Verluste dar und der Bereich oberhalb des Breake-Even-Punkts zeigt das Volumen des Gesamtgewinns. Dieses Diagramm kann verwendet werden, um den Gewinn auf verschiedenen Leistungsebenen zu identifizieren.

Annahmen zur CVP-Analyse

Obwohl die CVP-Analyse ein nützliches Instrument für das Management Accounting ist, sind ihre Schlussfolgerungen nur gültig, wenn die folgenden Annahmen getroffen wurden halten:

• Alle Kosten können als variabel oder fest eingestuft werden. Zu diesem Zweck werden gemischte Kosten unter Verwendung von Techniken wie High-Low-Methode, Streudiagrammmethode und Regressionsanalyse in variable und feste Komponenten aufgeteilt.
• Der Verkaufspreis pro Einheit, die variablen Kosten pro Einheit und die gesamten Fixkosten sind konstant . Diese Annahme ist problematisch, da Skaleneffekte bestehen, die Skalenerträge steigen / sinken und der Lernkurveneffekt.
• Alle Einnahmen und Kosten stehen in einem linearen Verhältnis zum Volumen.
• Der Umsatz Der Mix eines Unternehmens bleibt konstant.

von Irfanullah Jan, ACCA und zuletzt geändert am 2. Oktober 2020