Die Poincaré-Vermutung und 6 andere komplexe mathematische Theorien wurden vom Clay Mathematics Institute (CMI) als Millennium-Preis-Probleme bezeichnet. Jedes Problem wurde als „wichtige klassische Frage, die sich im Laufe der Jahre gegen Lösungen gewehrt hat“ beschrieben, wobei die erste Person eine Lösung für jedes Problem entwickelte, das mit freundlicher Genehmigung des CMI 1.000.000 US-Dollar einbrachte. Wie Sie oben gesehen haben, ist die Lösung dieser Probleme jedoch nicht einfach feat. Eines der Probleme ist seit seiner Formulierung im Jahr 1859 durch den deutschen Mathematiker Bernhard Riemann ungelöst geblieben.
Die Riemann-Hypothese, benannt nach dem oben genannten deutschen Mathematiker, wird allgemein als das wichtigste ungelöste Problem im reinen Bereich angesehen Mathematik. Es ist von großem Interesse für die Zahlentheorie, da es Ergebnisse über die Verteilung von Primzahlen impliziert, die in allen Bereichen von Biologie über Verschlüsselung bis hin zur Quantenmechanik verwendet werden. Um die Riemann-Hypothese zu verstehen, müssen wir zunächst einige Schlüssel erklären Konzepte:
- Eine komplexe Zahl hat die Form a + bi, wobei i durch i² = -1 definiert ist. In dieser Form ist der Realteil einer komplexen Zahl a und das Imaginäre Teil ist bi.
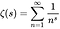
- Eine „Null“ einer Funktion ist ein x, so dass f (x) = 0
- Die „trivialen Nullen“ der Riemannschen Zeta-Funktion sind alle negativen geraden ganzen Zahlen (-2, -4, -6, …)
- Die „nicht trivialen Nullen“ ”Der Riemannschen Zeta-Funktion sind alle anderen Werte von s, für die ζ (s) = 0 (dh. s ist keine negative gerade Ganzzahl).
Nachdem wir einige Definitionen festgelegt haben, können wir die Riemann-Hypothese aufstellen:
Der Realteil jeder nicht trivialen Null der Riemannschen Zeta-Funktion ist 1/2
Dieser (für mich) Zumindest) ist viel einfacher zu verstehen als die Poincaré-Vermutung und scheint intuitiv nicht sehr schwierig zu sein. Es scheint jedoch auch nicht viel zu bedeuten. Wirklich, wen interessiert es, wenn diese Zufallsfunktion den Wert 0 hat? Nun, nicht überraschend, viele Mathematiker tun dies aus einem sehr guten Grund.
Einige Zahlen haben die besondere Eigenschaft, dass sie nicht ausgedrückt werden können als Produkt zweier kleinerer Zahlen (Produkt ist Multiplikation), dh. 2,3,5,7,11 usw. Bekannt als Primzahlen, sind sie gewissermaßen die einfachsten Zahlen, die Sie bekommen können, und bilden die Bausteine für alle anderen Zahlen. Es ist jedoch frustrierend, dass Primzahlen keinem Muster folgen. 3137 ist eine Primzahl, und die nächste danach ist erst 3163, aber dann folgen 3167 und 3169 in schneller Folge, die alle Primzahlen sind. Kurz gesagt, wenn Sie eine Primzahl finden, können Sie nicht sagen, wo die nächste sein wird, ohne alle Zahlen zu überprüfen. Mithilfe des Primzahlsatzes (PNT) können Sie jedoch ermitteln, wie viele Primzahlen unterhalb eines bestimmten Schwellenwerts liegen.
Der Primzahlsatz ist nur eine Schätzung, wobei unterschiedliche Werte eine unterschiedliche Wahrscheinlichkeit des Seins ergeben richtig, aber niemals 100% ige Sicherheit. Wenn Sie jedoch die Annahme verstehen, dass die Reimann-Hypothese wahr ist, können Sie eine mathematische Näherung erstellen, die den Primzahlsatz und die nicht trivialen Nullen der Riemannschen Zeta-Funktion kombiniert, um die internen Komponenten fehlerkorrigieren zu können und die „bestmögliche“ Grenze für bereitzustellen Der Fehlerterm im Primzahlsatz. Wenn es möglich wäre, die Reimann-Hypothese vollständig zu beweisen, würde dies der PNT die Möglichkeit geben, unglaublich genaue Schätzungen des tatsächlichen Werts zu liefern, was viele Möglichkeiten in verschiedenen Bereichen der Mathematik eröffnet. Es gibt viele wichtige Hypothesen, die mit „Wenn die Riemann-Hypothese wahr ist, dann …“ übereinstimmen. Wenn Sie also dieses Problem lösen, werden auch alle nachfolgenden Vermutungen sofort bestätigt.