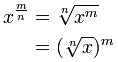Også kalt «Radikale» eller «Rasjonelle eksponenter»
Eksponenter for hele antall
La oss først se på hele tallet eksponenter:

Eksponenten av et tall sier hvor mange ganger tallet skal brukes i en multiplikasjon.
I dette eksemplet: 82 = 8 × 8 = 64
Et annet eksempel: 53 = 5 × 5 × 5 = 125
Brøkeksponenter
Men hva om eksponenten er en brøkdel?
|
En eksponent på 12 er faktisk kvadratrot En eksponent på 13 er terningsrot En eksponent på 14 er 4. rot Og så videre! |
 |
Hvorfor?
La oss se hvorfor i en eksempel.
For det første forteller lovene om eksponenter hvordan vi skal håndtere eksponenter når vi multipliserer:
Eksempel: x2x2 = (xx) (xx) = xxxx = x4
Som viser at x2x2 = x (2 + 2) = x4
Så la oss prøve det med fraksjonelle eksponenter:
Prøv en annen brøk
La oss prøve det igjen, men med en eksponent på en fjerdedel (1/4):
Eksempel:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Så 16¼ brukt 4 ganger i en multiplikasjon gir 16,
og så er 16¼ en 4. rot av 16
Generell regel
Det fungerte i ½, det fungerte med ¼, faktisk fungerer det generelt:
x1 / n = Den niende roten til x
Så vi kan finne på dette:
| |
|
Eksempel: Hva er 271/3?
Svar: 271/3 = ![]() 27 = 3
27 = 3
Hva med mer kompliserte brøker?
Hva med en brøkeksponent som 43/2?
Det betyr egentlig å gjøre en kube (3) og en kvadratrot (1/2), i hvilken som helst rekkefølge.
La meg forklare.
En brøk (som m / n) kan deles i to deler:
- en hel talldel (m) og
- en brøk (1 / n) del
Så fordi m / n = m × (1 / n) kan vi gjøre dette:
Rekkefølgen spiller ingen rolle, så det fungerer også for m / n = (1 / n) × m:
Og vi får dette:
| |
|
Noen eksempler:
Eksempel : Hva er 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
eller
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
Uansett får det samme resultatet.
Eksempel: Hva er 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
eller
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
Det var absolutt lettere den andre veien!
Nå … Spill med grafen!
Se hvor jevnt kurven endres når du spiller med brøkene i denne animasjonen, dette viser deg at denne ideen om fraksjonelle eksponenter passer fint sammen:
Ting du kan prøve:
- Start med m = 1 og n = 1, og øk deretter sakte n slik at du kan se 1/2, 1/3 og 1/4
- Prøv deretter m = 2 og skyv n opp og ned for å se brøker som 2/3 osv.
- Prøv nå å gjøre eksponenten -1
- Til slutt prøver du å øke m, deretter redusere n, deretter redusere m, deretter øke n: kurven skal gå rundt og rundt