Glem alt du vet om tall.
Glem faktisk at du til og med vet hva et tall er.
Dette er der matematikk starter.
I stedet for matte med tall, vil vi nå tenke på matte med «ting».
Definisjon
Hva er et sett? Vel, rett og slett, det er en samling.
Først spesifiserer vi en felles egenskap blant «ting» (vi definerer dette ordet senere), og deretter samler vi alle «ting» som har denne felles eiendommen.

For eksempel varene du bruker: lue, skjorte, jakke, bukser , og så videre.
Jeg er sikker på at du kan komme med minst hundre.
Dette er kjent som et sett.
|
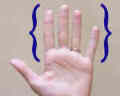
Eller et annet eksempel er typer fingre. Dette settet inkluderer indeks, midt, ring og rosa. |
 |
Så det er bare ting gruppert sammen med en bestemt egenskap til felles.
Notasjon
Det er en ganske enkel notasjon for sett. Vi lister ganske enkelt opp hvert element (eller «medlem») atskilt med komma, og setter så noen krøllete parenteser rundt det hele:

De krøllete parentesene {} kalles noen ganger «sette parenteser» eller «parenteser».
Dette er notasjonen for de to foregående eksemplene:
{sokker, sko, klokker, skjorter, …}
{index, middle, ring, pinky}
Legg merke til hvordan det første eksemplet har «…» (tre prikker sammen) .
De tre punktene … kalles en ellipse, og betyr «fortsett».
Så det betyr at det første eksemplet fortsetter … for uendelig.
(OK, det er ikke uendelig mye ting du kan ha på deg, men jeg er ikke helt sikker på det! Etter en times tenkning på forskjellige ting, jeg fortsatt ikke sikker. Så la oss bare si at det er uendelig for dette eksemplet.)
Så:
Men noen ganger kan «…» brukes i midten for å lagre skrive lange lister:
Eksempel: bokstavsettet:
{a, b, c, .. ., x, y, z}
I dette tilfellet er det et endelig sett (det er bare 26 bokstaver, ikke sant?)
Numeriske sett
Så hva har dette med matematikk å gjøre? Når vi definerer et sett, er alt vi trenger å spesifisere en felles karakteristikk. Hvem sier at vi ikke kan gjøre det med tall?
Og så videre. Vi kan komme opp med alle forskjellige typer sett.
Vi kan også definere et sett etter dets egenskaper, slik som {x | x > 0} som betyr «settet med alle x», slik at x er større enn 0 «, se Set-Builder Notation for å lære mer.
Og vi kan ha sett med tall som ikke har noen felles egenskap, de er bare definert på den måten. For eksempel:
{4, 5, 6, 10, 21}
{2, 949, 48282, 42882959, 119484203 }
Er alle sett som jeg bare tilfeldig banket på tastaturet mitt for å produsere.
Hvorfor er sett viktig?
Sett er den grunnleggende egenskapen til matematikk. Nå som et advarsel, virker sett i seg selv ganske meningsløse. Men det er bare når vi bruker sett i forskjellige situasjoner, blir de den kraftige byggesteinen i matematikk som de er.
Matematikk kan bli utrolig komplisert ganske raskt. Grafteori, abstrakt algebra, reell analyse, kompleks Analyse, lineær algebra, tallteori og listen fortsetter. Men det er en ting som alle disse deler til felles: sett.
Universal sett
 |
I begynnelsen brukte vi ordet «ting» i anførselstegn. Vi kaller dette det universelle settet. Det er et sett som inneholder alt. Vel, ikke akkurat alt. Alt som er relevant for spørsmålet vårt. |
|
 |
I Tallteori er universalsettet alle heltall, da Tallteori ganske enkelt er studie av heltall. |
|
 |
Men i Calculus (også kjent som reell analyse) er det universelle settet nesten alltid de reelle tallene. |
|
 |
Og i kompleks analyse gjettet du det, det universelle settet er de komplekse tallene. |
Noe mer notasjon
 |
Når vi snakker om sett, er det ganske standard å bruke store bokstaver for å representere settet, og små bokstaver for å representere et element i det settet. Så for eksempel er A et sett, og a er et element nt i A. Samme med B og b, og C og c. |
Nå trenger du ikke å lytte til standarden , kan du bruke noe som m til å representere et sett uten å bryte noen matematiske lover (pass opp, du kan få π år i matematisk fengsel for å dele med 0), men denne notasjonen er ganske fin og enkel å følge, så hvorfor ikke?
Når vi sier at et element a er i et sett A, bruker vi symbolet ![]() for å vise det.
for å vise det.
Og hvis noe ikke er i en sett bruk ![]() .
.
Eksempel: Sett A er {1,2,3}. Vi kan se at 1 ![]() A, men 5
A, men 5 ![]() A
A
Likhet
To sett er like hvis de har nøyaktig Nå ved første øyekast virker de kanskje ikke like, så vi må kanskje undersøke dem nøye!
Eksempel: Er A og B like hvor:
- A er settet hvis medlemmer er de første fire positive heltallene
- B = {4, 2, 1, 3}
La oss sjekke. De inneholder begge 1. De inneholder begge 2. Og 3, Og 4. Og vi har sjekket hvert element i begge settene, så: Ja, de er like!
Og likhetstegnet ( =) brukes til å vise likhet, så vi skriver:
A = B

Delsett
Når vi definerer et sett, hvis vi tar deler av det settet, kan vi danne det som kalles et delsett.
Generelt:
A er en delmengde av B hvis og bare hvis hvert element i A er i B.
Så la oss bruke denne definisjonen i noen eksempler.
La oss prøve et vanskeligere eksempel.
Riktige delmengder
Hvis vi ser på definisjonen av delmengder og lar tankene vandre litt, kommer vi til en merkelig konklusjon.
La A være et sett. Er hvert element av A i A?
Vel, umm, ja selvfølgelig, ikke sant?
Så det betyr at A er en delmengde av A. Det er en delmengde av seg selv!
Dette virker ikke veldig riktig, gjør det? Hvis vi vil at delmengdene våre skal være riktige, introduserer vi (hva annet enn) riktige delmengder:
A er en riktig delmengde av B hvis og bare hvis element av A er også i B, og det finnes minst ett element i B som ikke er i A.
Dette lille stykket på slutten er der for å sikre at A ikke er en riktig delsett av seg selv: vi sier at B må ha minst ett ekstra element.
Eksempel:
{1, 2, 3} er et delsett av {1, 2, 3}, men er ikke en riktig delmengde av {1, 2, 3}.
Eksempel:
{1, 2, 3} er en riktig delmengde av {1, 2, 3, 4} fordi elementet 4 ikke er i det første settet.
Legg merke til at når A er en riktig delmengde av B, er det også en delmengde av B.
Enda mer notasjon
Når vi sier at A er en delmengde av B, skriver vi A ![]() B.
B.
Eller vi kan si at A ikke er en delmengde av B av A ![]() B («A er ikke en delmengde av B»)
B («A er ikke en delmengde av B»)
Når vi snakker om riktige delmengder, vi tar ut linjen under og så blir det A ![]() B eller hvis vi vil si det motsatte, A
B eller hvis vi vil si det motsatte, A ![]() B.
B.
Tomt (eller null) sett
Dette er sannsynligvis det rareste med sett.

Tenk på settet med pianotaster på en gitar.
«Men vent!» du sier, «Det er ingen pianotaster på en gitar! «
Og det er riktig. Det er et sett uten elementer.
Dette er kjent som Tomt sett (eller Nullsett). Det er ikke noen elementer i det. Ikke ett. Null.
Det representeres av ![]()
Eller av {} (et sett uten elementer)
Noen andre eksempler på det tomme settet er settet av land sør for sørpolen.
Så hva er så rart med det tomme settet? Vel, den delen kommer neste gang.
Tomt sett og delsett
Så la oss gå tilbake til vår definisjon av delmengder. Vi har et sett A. Vi vil ikke definere det noe mer enn det, det kan være noe sett. Er det tomme settet en delmengde av A?
Går vi tilbake til vår definisjon av delmengder, hvis hvert element i det tomme settet også er i A, så er det tomme settet en delmengde av A. Men hva om vi har ingen elementer?
Det krever en introduksjon til logikken for å forstå dette, men denne påstanden er en som er «vakuum» eller «trivielt» sant.
En god måte å tenke på det er: vi kan ikke finne noen elementer i det tomme settet som ikke er i A, så det må være at alle elementene i det tomme settet er i A.
Så svaret på det stilte spørsmålet er et rungende ja.
Det tomme settet er en delmengde av hvert sett, inkludert selve det tomme settet.
Bestilling
Nei, ikke rekkefølgen av elementene. I sett spiller det ingen rolle hvilken rekkefølge elementene er i.
Eksempel: {1,2,3,4} er det samme settet som {3,1,4,2}
Når vi sier rekkefølge i sett, mener vi størrelsen på settet.
Et annet (bedre) navn på dette er kardinaliteten.
Et endelig sett har endelig rekkefølge (eller kardinalitet). Et uendelig sett har uendelig rekkefølge (eller kardinalitet).
For endelige sett er rekkefølgen (eller kardinaliteten) antall elementer.
Eksempel: {10, 20, 30, 40} har en rekkefølge på 4.
For uendelige sett kan vi bare si at rekkefølgen er uendelig. Merkelig nok kan vi si med sett at noen uendeligheter er større enn andre, men dette er et mer avansert tema i sett.
Arg! Ikke mer notasjon!
Nei, bare tuller. Ikke mer notasjon.
av
og