Hva er standardavvik? | STDEV.P | STDEV.S | Variasjon
Denne siden forklarer hvordan man beregner standardavviket basert på hele populasjonen ved hjelp av STDEV.P-funksjonen i Excel, og hvordan man estimerer standardavviket basert på et utvalg ved hjelp av STDEV.S-funksjonen i Excel.
Hva er standardavvik?
Standardavvik er et tall som forteller deg hvor langt tall er fra gjennomsnittet.
1. For eksempel har tallene nedenfor et gjennomsnitt (gjennomsnitt) på 10.
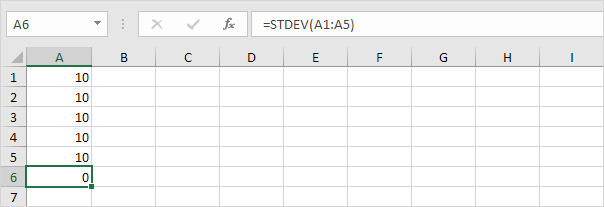
Forklaring: tallene er alle de samme som betyr at det ikke er noen variasjon. Som et resultat har tallene et standardavvik på null. STDEV-funksjonen er en gammel funksjon. Microsoft Excel anbefaler at du bruker den nye STEDV.S-funksjonen som gir nøyaktig samme resultat.
2. Tallene nedenfor har også et gjennomsnitt (gjennomsnitt) på 10.
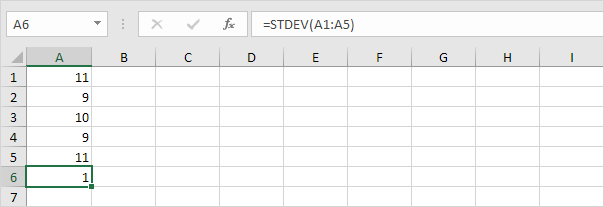
Forklaring: tallene er nær gjennomsnittet. Som et resultat har tallene et lavt standardavvik.
3. Tallene nedenfor har også et gjennomsnitt (gjennomsnitt) på 10.
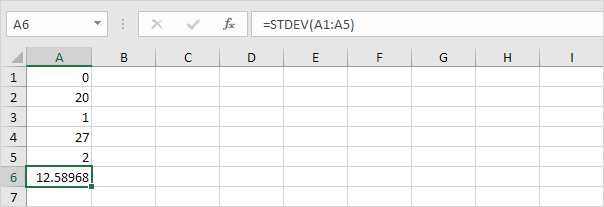
Forklaring: tallene er spredt. Som et resultat har tallene et høyt standardavvik.
STDEV.P
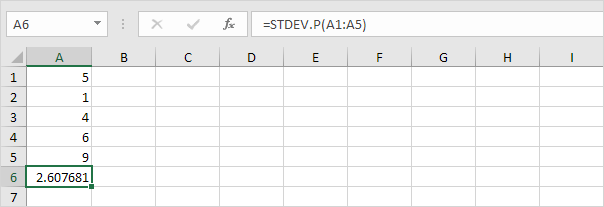
STDEV.P-funksjonen (P står for Befolkning) i Excel beregner standardavviket basert på hele befolkningen. For eksempel lærer du en gruppe på 5 studenter. Du har testresultatene til alle studenter. Hele befolkningen består av 5 datapunkter. STDEV.P-funksjonen bruker følgende formel:
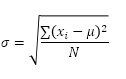
I dette eksemplet er x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (gjennomsnitt), N = 5 (antall datapunkter).
1. Beregn gjennomsnittet (μ).
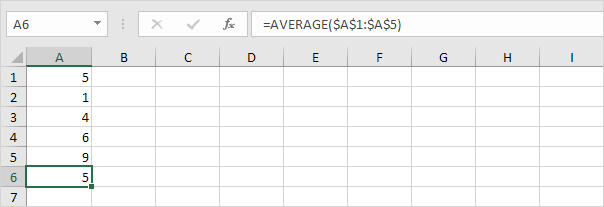
2. For hvert tall beregner du avstanden til gjennomsnittet.
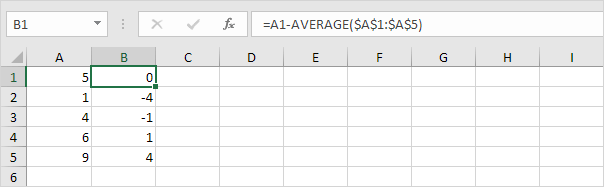
3. Kvadrerer denne avstanden for hvert tall.
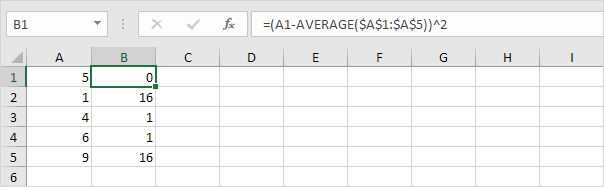
4. Sum (∑) disse verdiene.
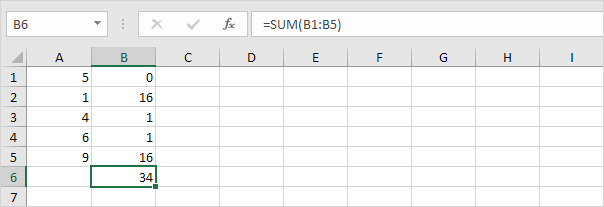
5. Del med antall datapunkter (N = 5).
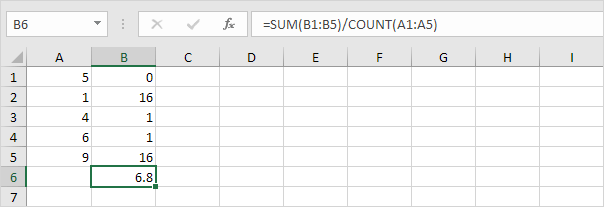
6. Ta kvadratroten.
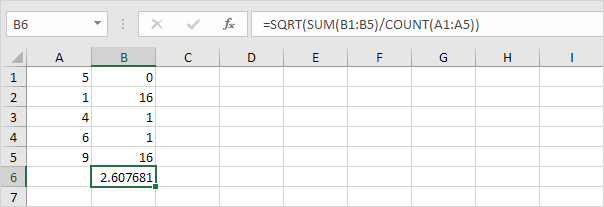
7. Heldigvis kan STDEV.P-funksjonen i Excel utføre alle disse trinnene for deg.
STDEV.S
STDEV.S-funksjonen (S står for Sample) i Excel estimerer standardavviket basert på et utvalg. For eksempel lærer du en stor gruppe studenter. Du har bare testresultatene på 5 studenter. Eksempelstørrelsen er lik 5. STDEV.S-funksjonen bruker følgende formel:
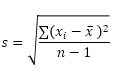
I dette eksemplet er x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (samme tall som ovenfor), x̄ = 5 (eksempel gjennomsnitt), n = 5 (prøvestørrelse).
1. Gjenta trinn 1-5 ovenfor, men ved trinn 5 divider med n-1 i stedet for N.
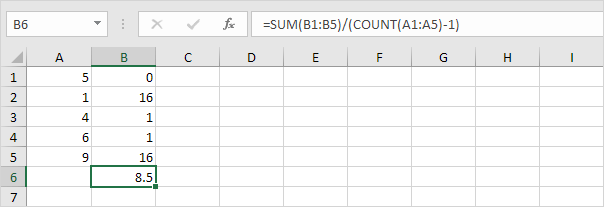
2. Ta kvadratroten.
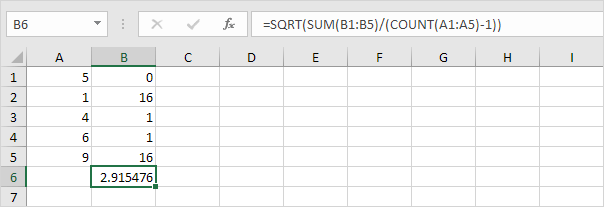
3. Heldigvis kan STDEV.S-funksjonen i Excel utføre alle disse trinnene for deg.
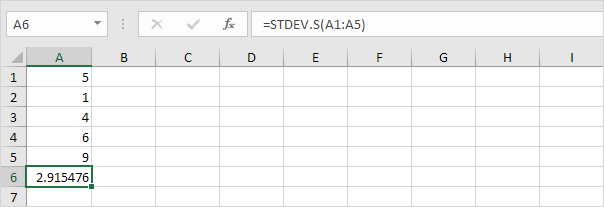
Merk: hvorfor deler vi etter n – 1 i stedet for ved n når vi estimerer standardavviket basert på et utvalg? Bessels korreksjon sier at å dele med n-1 i stedet for med n gir et bedre estimat av standardavviket.
Varianse
Variasjon er kvadratet til standardavviket. Det er så enkelt. Noen ganger er det lettere å bruke avviket når man skal løse statistiske problemer.
1. VAR.P-funksjonen nedenfor beregner variansen basert på hele befolkningen.
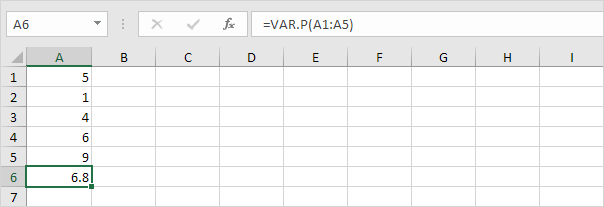
Merk: du visste allerede dette svaret (se trinn 5 under STDEV.P). Ta kvadratroten av dette resultatet for å finne standardavviket basert på hele populasjonen.
2. VAR.S-funksjonen nedenfor estimerer variansen basert på et utvalg.
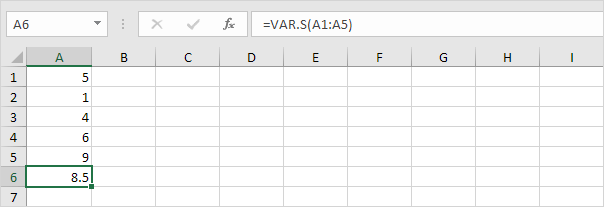
Merk: du visste allerede dette svaret (se trinn 1 under STDEV.S). Ta kvadratroten av dette resultatet for å finne standardavviket basert på et utvalg.
3. VAR og VAR.S gir nøyaktig samme resultat.
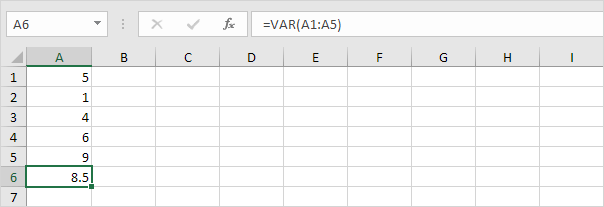
Merk: Microsoft Excel anbefaler at du bruker den nye VAR.S-funksjonen.