Poincaré-formodningen og 6 andre komplekse matematiske teorier er blitt kalt Millennium Prize Problems av Clay Mathematics Institute (CMI). Hvert problem har blitt beskrevet som et «viktig klassisk spørsmål som har motstått løsninger gjennom årene», med den første personen som utviklet en løsning for hver som tjener $ 1 000 000 med tillatelse fra CMI. Som du så ovenfor, er det ikke lett å løse disse problemene. feat. Et av problemene har vært uløst siden den ble formulert i 1859 av den tyske matematikeren Bernhard Riemann.
Riemann-hypotesen, oppkalt etter den nevnte tyske matematikeren, anses allment for å være det viktigste uløste problemet i ren matematikk. Det er av stor interesse for tallteori fordi det innebærer resultater om fordelingen av primtall, som brukes i alt fra biologi til kryptering og kvantemekanikk. For å forstå Riemann-hypotesen, må vi først forklare noen få nøkkel begreper:
- Et komplekst tall er av formen a + bi, hvor i er definert av i² = -1. I denne formen er den virkelige delen av et komplekst tall a, og det imaginære del er bi.
- Riemann zeta-funksjonen er en funksjon av en kompleks variabel (en funksjon av komplekse tall) definert av følgende ligning, der s er et hvilket som helst annet kompleks enn 1, og hvis verdier også er komplekse:
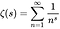
- En «null» av en funksjon er en x slik at f (x) = 0
- De «trivielle nullene» til Riemann zeta-funksjonen er alle de negative, heltallene (-2, -4, -6,…)
- De «ikke-trivielle nullene ”Av Riemann zeta-funksjonen er alle de andre verdiene til s der ζ (s) = 0 (dvs. s er ikke et negativt, heltall).
Nå som vi har noen definisjoner nede, kan vi gå videre og angi Riemann-hypotesen:
Den virkelige delen av ethvert ikke-trivielt null i Riemann zeta-funksjonen er 1/2
Denne (for meg i det minste) er mye lettere å forstå enn Poincaré Conjecture og virker ikke intuitivt veldig vanskelig. Imidlertid ser det ikke ut til å bety mye. Virkelig, hvem bryr seg om når denne tilfeldige funksjonen har verdien 0. Vel, ikke overraskende, mange matematikere gjør det, og av en veldig god grunn.
Noen tall har den spesielle egenskapen at de ikke kan uttrykkes. som produktet av to mindre tall (produktet blir multiplikasjon), dvs. 2,3,5,7,11 osv. Kjent som primtall, de er på en måte de enkleste tallene du kan få, og danner byggesteinene for alle andre tall. Frustrerende skjønt, primtall ser ikke ut til å følge noe mønster. 3137 er et primtall, og det neste etter det er ikke før 3163, men deretter følger 3167 og 3169 i rask rekkefølge, som alle er primtall. I et nøtteskall, hvis du finner ett primtall, er det ingen måte å fortelle hvor den neste kommer til å være uten å sjekke alle tallene mens du går. Ved å bruke Prime Number Theorem (PNT), kan du finne hvor mange primtall det er under en viss terskel.
Prime Number Theorem er bare en estimering, med forskjellige verdier som gir en annen sannsynlighet for å være riktig, men aldri 100% sikkerhet. Forstå imidlertid antagelsen om at Reimann-hypotesen er sant, du kan lage en matematisk tilnærming som kombinerer primtallsetningen og de ikke-trivielle nullene til Riemann zeta-funksjonen for å feilkorrigere de interne komponentene, og gir den «best mulig» bundet for feiluttrykket i Prime Number Theorem. Hvis det var mulig å bevise Reimann-hypotesen fullstendig, ville dette gitt PNT muligheten til å gi utrolig nære estimater til den faktiske verdien, og åpne for mange muligheter innen forskjellige grener av matematikken. det er mange viktige hypoteser om at det å være med «Hvis Riemann-hypotesen er sant, så …», så å løse dette problemet vil også umiddelbart validere alle påfølgende antagelser.