Teraz, gdy wiesz już, jak mnożyć liczby całkowite, dzielenie liczb całkowitych powinno być proste. Powodem jest to, że przestrzegają tych samych zasad.
Reguły o tym, jak dzielić liczby całkowite
Krok 1: Podziel ich wartości bezwzględne.
Krok 2: Określ znak ostatecznej odpowiedzi (zwanej ilorazem), korzystając z następujących warunków.
- Warunek 1: jeśli znaki obu liczb są takie same, iloraz jest zawsze liczbą dodatnią.
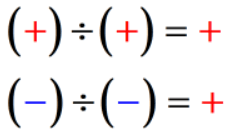
- Warunek 2: jeśli znaki dwóch liczb są różne, iloraz jest zawsze liczbą ujemną.
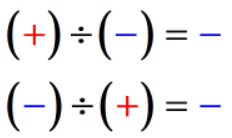
Przykłady dzielenia liczb całkowitych
Przykład 1: podzielenie dwóch liczb całkowitych poniżej.
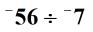
Rozwiązanie: Najpierw znajdź wartości bezwzględne dwóch liczb całkowitych.
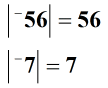
Następnie podziel liczby lub znajdź ich iloraz .
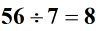
Na koniec określ ostateczny znak odpowiedzi lub iloraz. Ponieważ dzielimy dwie liczby całkowite tym samym znakiem, iloraz będzie miał znak dodatni.
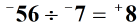
Przykład 2: Podziel poniższe dwie liczby całkowite.
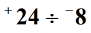
Rozwiązanie: podziel wartości bezwzględne dwóch liczb całkowitych.
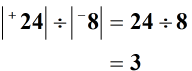
Zgodnie z powyższymi zasadami, podczas dzielenia liczb całkowitych z różnymi oznacza, że ostateczna odpowiedź (iloraz) jest ujemna.
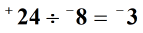
Przykład 3: Podziel poniższe trzy liczby całkowite od lewej do prawej
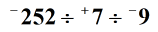
Rozwiązanie: Aby podzielić trzy lub więcej liczb całkowitych, ważne jest, aby wykonać operację dzielenia od lewej do prawej. Ponadto możemy to osiągnąć, dzieląc jednocześnie dwie liczby całkowite. Nawiasy pokazują pierwsze dwie liczby całkowite do podzielenia, a wynik lub iloraz zostanie podzielony przez następną. Mamy tutaj: – 252 podzielone przez + 7 równa się – 36. Jest to iloraz ujemny, ponieważ dzielimy dwie liczby całkowite, które mają różne znaki. Następnie bierzemy ten iloraz i dzielimy go przez następującą liczbę całkowitą. Otrzymujemy –36 ÷ –9 = + 4.
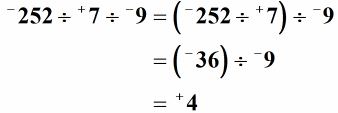
Ćwicz z arkuszami roboczymi
Możesz być także zainteresowany:
Dodawanie liczb całkowitych
Odejmowanie liczb całkowitych
Mnożenie liczb całkowitych