Co to jest odchylenie standardowe? | STDEV.P | STDEV.S | Wariancja
Na tej stronie wyjaśniono, jak obliczyć odchylenie standardowe na podstawie całej populacji przy użyciu funkcji ODCH.STANDARDOWE w programie Excel i jak oszacować odchylenie standardowe na podstawie próbki przy użyciu funkcji ODCH.STANDARDOWE w programie Excel.
Co to jest odchylenie standardowe?
Odchylenie standardowe to liczba, która mówi, jak daleko liczby są od średniej.
1. Na przykład poniższe liczby mają średnią (średnią) 10.
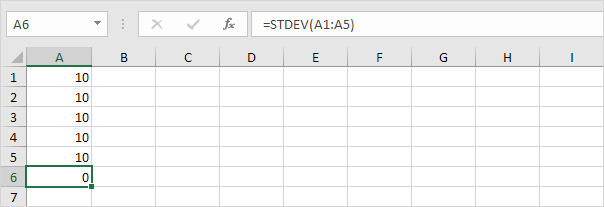
Wyjaśnienie: wszystkie liczby są takie same, co oznacza brak odchyleń. W rezultacie liczby mają odchylenie standardowe równe zero. Funkcja ODCH. STANDARDOWE jest starą funkcją. Microsoft Excel zaleca użycie nowej funkcji STEDV.S, która daje dokładnie taki sam wynik.
2. Poniższe liczby również mają średnią (średnią) 10.
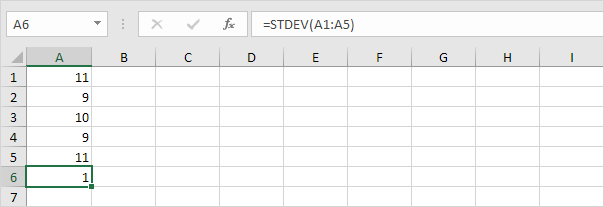
Wyjaśnienie: liczby są bliskie średniej. W rezultacie liczby mają niskie odchylenie standardowe.
3. Poniższe liczby mają również średnią (średnią) 10.
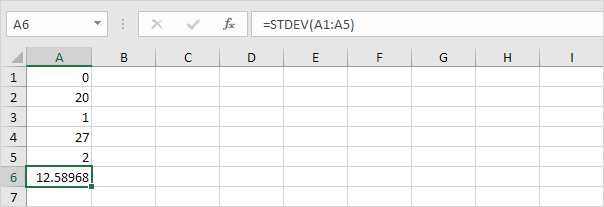
Wyjaśnienie: liczby są rozłożone. W rezultacie liczby mają wysokie odchylenie standardowe.
STDEV.P
Funkcja STDEV.P (P oznacza populację) w programie Excel oblicza odchylenie standardowe na podstawie całej populacji. Na przykład „uczysz grupę 5 uczniów. Masz wyniki testów wszystkich uczniów. Cała populacja składa się z 5 punktów danych. Funkcja STDEV.P używa następującej formuły:
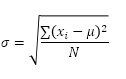
W tym przykładzie x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (średnia), N = 5 (liczba punktów danych).
1. Oblicz średnią (μ).
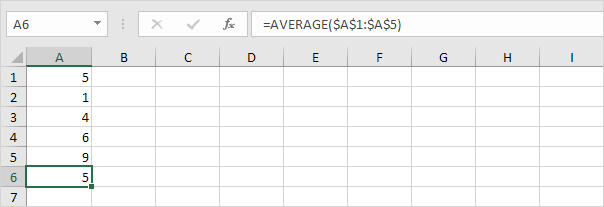
2. Dla każdej liczby oblicz odległość do średniej.
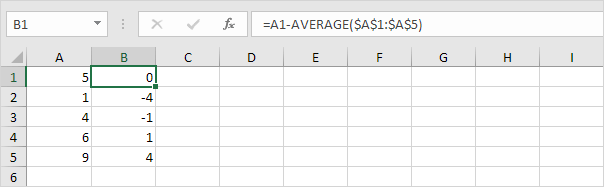
3. Dla każdej liczby wyrównaj tę odległość do kwadratu.
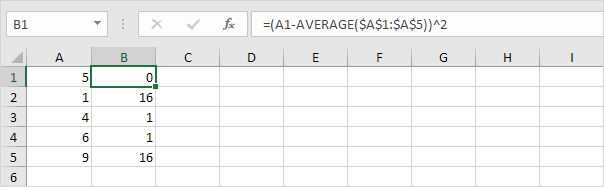
4. Zsumuj (∑) te wartości.
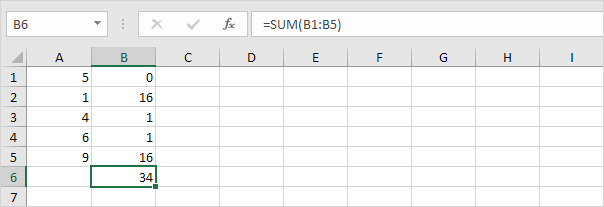
5. Podziel przez liczbę punktów danych (N = 5).
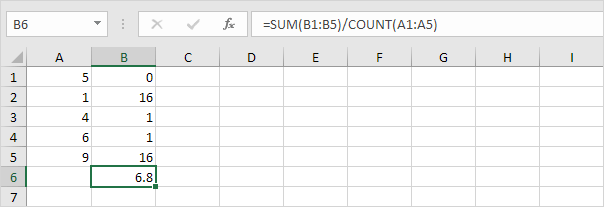
6. Weź pierwiastek kwadratowy.
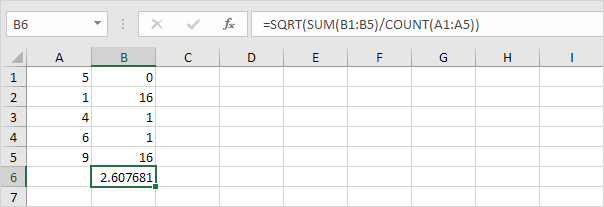
7. Na szczęście funkcja STDEV.P w programie Excel może wykonać wszystkie te czynności.
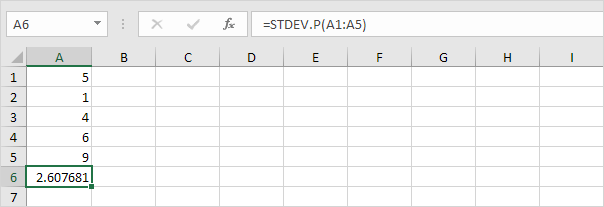
STDEV.S
Funkcja ODCH.STANDARDOWE (S oznacza próbkę) w programie Excel szacuje odchylenie standardowe na podstawie próbki. Na przykład „uczysz dużą grupę uczniów. Masz tylko 5 uczniów na teście. Wielkość próby jest równa 5. Funkcja ODCH.STANDARDOWE używa następującego wzoru:
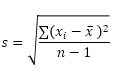
W tym przykładzie x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (te same liczby co powyżej), x̄ = 5 (próbka średnia), n = 5 (wielkość próbki).
1. Powtórz powyższe kroki 1-5, ale w kroku 5 podziel przez n-1 zamiast N.
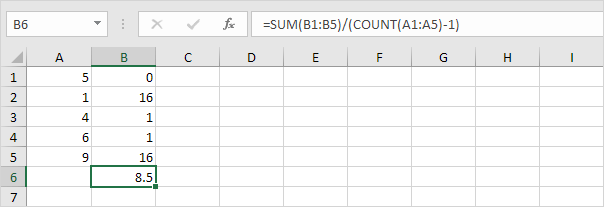
2. Weź pierwiastek kwadratowy.
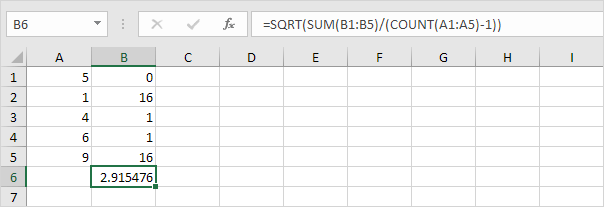
3. Na szczęście funkcja STDEV.S w programie Excel może wykonać wszystkie te kroki.
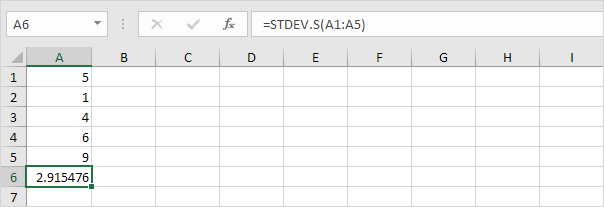
Uwaga: dlaczego dzielimy przez n – 1 zamiast przez n, gdy szacujemy odchylenie standardowe na podstawie próbki? Poprawka Bessela stwierdza, że dzielenie przez n-1 zamiast przez n daje lepsze oszacowanie odchylenia standardowego.
Wariancja
Wariancja to kwadrat odchylenia standardowego. To takie proste. Czasami łatwiej jest użyć wariancji podczas rozwiązywania problemów statystycznych.
1. Poniższa funkcja VAR.P oblicza wariancję na podstawie całej populacji.
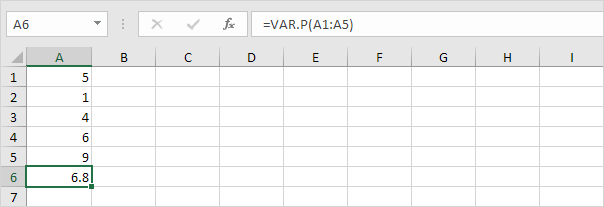
Uwaga: znasz już tę odpowiedź (zobacz krok 5 w STDEV.P). Weź pierwiastek kwadratowy z tego wyniku, aby znaleźć odchylenie standardowe na podstawie całej populacji.
2. Poniższa funkcja VAR.S szacuje wariancję na podstawie próbki.
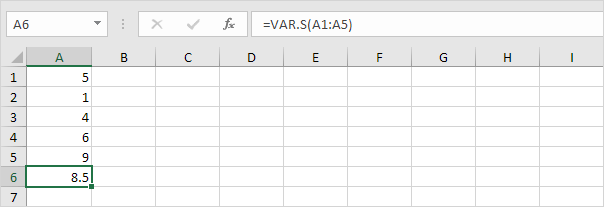
Uwaga: znasz już tę odpowiedź (zobacz krok 1 w ramach STDEV.S). Weź pierwiastek kwadratowy z tego wyniku, aby znaleźć odchylenie standardowe na podstawie próbki.
3. WARIANCJA i WARIANCJA.S.dają dokładnie ten sam wynik.
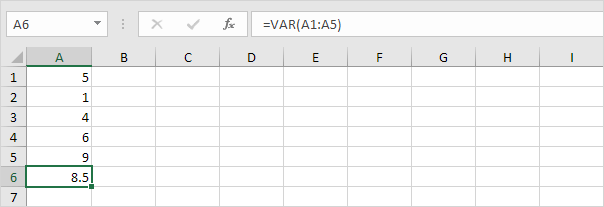
Uwaga: Microsoft Excel zaleca używanie nowej funkcji WARIANCJA.S.