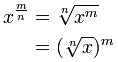Nazywane także „rodnikami” lub „wymiernymi wykładnikami”
Potęgi liczb całkowitych
Najpierw przyjrzyjmy się liczbie całkowitej wykładniki:

Wykładnik liczby mówi, ile razy należy użyć liczby w mnożeniu.
W tym przykładzie: 82 = 8 × 8 = 64
Inny przykład: 53 = 5 × 5 × 5 = 125
Ułamkowe wykładniki potęgowe
Ale co, jeśli wykładnik jest ułamkiem?
|
Wykładnik 12 to w rzeczywistości pierwiastek kwadratowy Wykładnik 13 to pierwiastek sześcienny Wykładnik 14 to czwarty pierwiastek I tak dalej! |
 |
Dlaczego?
Zobaczmy, dlaczego w przykład.
Po pierwsze, prawa wykładników mówią nam, jak postępować z wykładnikami podczas mnożenia:
Przykład: x2x2 = (xx) (xx) = xxxx = x4
Co pokazuje, że x2x2 = x (2 + 2) = x4
Spróbujmy to z ułamkowymi wykładnikami:
Wypróbuj inny ułamek
Spróbujmy jeszcze raz, ale z wykładnikiem jednej czwartej (1/4):
Przykład:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Czyli 16¼ użyte 4 razy w mnożeniu daje 16,
a więc 16¼ to a Czwarty pierwiastek z 16
Ogólna reguła
Działało dla ½, działało z ¼, w rzeczywistości działa ogólnie:
x1 / n = N-ty pierwiastek x
Więc możemy wymyślić to:
| |
|
Przykład: Co to jest 271/3?
Odpowiedź: 271/3 = ![]() 27 = 3
27 = 3
A co z bardziej skomplikowanymi ułamkami?
A co z wykładnikiem ułamkowym, takim jak 43/2?
To naprawdę mówi, żeby zrobić sześcian (3) i pierwiastek kwadratowy (1/2), w dowolnej kolejności.
Pozwólcie, że wyjaśnię.
Ułamek (np. m / n) można podzielić na dwie części:
- część całkowitą (m) i
- ułamek (1 / n) część
Tak więc, ponieważ m / n = m × (1 / n) możemy to zrobić:
Kolejność nie ma znaczenia, więc działa również dla m / n = (1 / n) × m:
I otrzymujemy to:
| |
|
Kilka przykładów:
Przykład : Co to jest 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
lub
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
W każdym przypadku otrzymujemy ten sam wynik.
Przykład: co to jest 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
lub
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
Drugi sposób z pewnością był łatwiejszy!
Teraz … Graj z wykresem!
Zobacz, jak płynnie zmienia się krzywa, gdy grasz ułamkami ta animacja pokazuje, że idea ułamkowych wykładników ładnie do siebie pasuje:
Rzeczy do wypróbowania:
- Zacznij od m = 1 i n = 1, a następnie powoli zwiększaj n, aby zobaczyć 1/2, 1/3 i 1/4
- Następnie spróbuj m = 2 i przesuń n w górę iw dół, aby zobaczyć ułamki, takie jak 2/3 itd.
- Teraz spróbuj zrobić wykładnik -1
- Na koniec spróbuj zwiększyć m, następnie zmniejszyć n, następnie zmniejszyć m, a następnie zwiększyć n: krzywa powinna krążyć wokół i wokół