Zapomnij o wszystkim, co wiesz o liczbach.
Zapomnij, że nawet wiesz, czym jest liczba.
To tam zaczyna się matematyka.
Zamiast matematyki z liczbami, będziemy teraz myśleć o matematyce z „rzeczami”.
Definicja
Co to jest zestaw? Cóż, po prostu jest to zbiór.
Najpierw określamy wspólną właściwość wśród „rzeczy” (określamy to słowo później), a następnie zbieramy wszystkie „rzeczy”, które mają tę wspólną własność.

Na przykład rzeczy, które nosisz: czapka, koszula, kurtka, spodnie i tak dalej.
Jestem pewien, że możesz wymyślić co najmniej sto.
To jest zbiór.
|
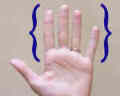
Albo inny przykład to rodzaje palców. Ten zestaw zawiera indeks, środek, pierścień i pinky. |
 |
Więc to są tylko rzeczy zgrupowane razem z pewną wspólną własnością.
Notacja
Jest dość prosta notacja zbiorów. Po prostu podajemy każdy element (lub „element członkowski”) oddzielony przecinkiem, a następnie umieszczamy kilka nawiasów klamrowych wokół całości:

Nawiasy klamrowe {} są czasami nazywane „nawiasami ustalającymi” lub „nawiasami klamrowymi”.
To jest notacja dwóch poprzednich przykładów:
{skarpetki, buty, zegarki, koszule, …}
{index, middle, ring, pinky}
Zwróć uwagę, że pierwszy przykład ma znak „…” (trzy kropki razem) .
Trzy kropki … nazywane są wielokropkiem i oznaczają „kontynuuj”.
Oznacza to, że pierwszy przykład jest kontynuowany. . na nieskończoność.
(OK, tak naprawdę nie ma nieskończonej liczby rzeczy, które można by założyć, ale nie jestem tego do końca pewien! Po godzinie rozmyślania o różnych rzeczach jestem nadal nie jestem pewien. Powiedzmy, że w tym przykładzie jest nieskończony.)
Więc:
Ale czasami można użyć „…” w środku, aby zapisać pisanie długich list:
Przykład: zestaw liter:
{a, b, c, .. ., x, y, z}
W tym przypadku jest to zbiór skończony (jest tylko 26 liter, prawda?)
Zestawy liczbowe
Więc co to ma wspólnego z matematyką? Kiedy definiujemy zbiór, musimy jedynie określić wspólną cechę. Kto powiedział, że nie możemy tego zrobić z liczbami?
I tak dalej. Możemy wymyślić różne typy zbiorów.
Możemy również zdefiniować zbiór na podstawie jego właściwości, takie jak {x | x > 0}, co oznacza „zbiór wszystkich x”, taki, że x jest większe niż 0 ”, zobacz Notacja Set-Builder, aby dowiedzieć się więcej.
I możemy mieć zbiory liczb, które nie mają wspólnej własności, są po prostu zdefiniowane w ten sposób. Na przykład:
{4, 5, 6, 10, 21}
{2, 949, 48282, 42882959, 119484203 }
Czy wszystkie zestawy, które po prostu losowo uderzyłem na klawiaturze, aby utworzyć.
Dlaczego zestawy są ważne?
Zbiory są podstawową właściwością matematyki. Teraz, jako słowo ostrzeżenia, zestawy same w sobie wydają się całkiem bezcelowe. Ale dopiero wtedy, gdy stosujemy zbiory w różnych sytuacjach, stają się one potężnym budulcem matematyki.
Matematyka może stać się niesamowicie skomplikowana dość szybko. Teoria grafów, algebra abstrakcyjna, analiza rzeczywista, zespolenie Analiza, algebra liniowa, teoria liczb i lista jest długa. Ale jest jedna rzecz, która łączy je wszystkie: zbiory.
Zbiór uniwersalny
 |
Na początku użyliśmy słowa „rzeczy” w cudzysłowie. Nazywamy to zbiorem uniwersalnym. Jest to zbiór zawierający wszystko. Cóż, nie do końca wszystko. Wszystko, co dotyczy naszego pytania. |
|
 |
W teorii liczb uniwersalny zbiór to wszystkie liczby całkowite, ponieważ teoria liczb to po prostu badanie liczb całkowitych. |
|
 |
Ale w Calculus (znanym również jako analiza rzeczywista) uniwersalnym zestawem są prawie zawsze liczby rzeczywiste. |
|
 |
A w analizie złożonej zgadłeś, uniwersalnym zbiorem są liczby zespolone. |
Więcej notacji
 |
Mówiąc o zestawach, dość standardowo używa się wielkich liter do przedstawienia zestawu, a małych liter do przedstawienia element w tym zbiorze. Na przykład A to zbiór, a a to element nt w A. To samo z B i b oraz C i c. |
Teraz nie musisz słuchać standardu , możesz użyć czegoś takiego jak m do reprezentowania zbioru bez łamania jakichkolwiek praw matematycznych (uważaj, możesz dostać π lat w więzieniu matematycznym za dzielenie przez 0), ale ten zapis jest całkiem ładny i łatwy do naśladowania, więc dlaczego nie?
Ponadto, gdy mówimy, że element a należy do zbioru A, używamy symbolu ![]() , aby go pokazać.
, aby go pokazać.
A jeśli czegoś nie ma w ustaw użyj ![]() .
.
Przykład: Zestaw A to {1,2,3}. Widzimy, że 1 ![]() A, ale 5
A, ale 5 ![]() A
A
Równość
Dwa zbiory są równe, jeśli mają dokładnie ci sami członkowie. Na pierwszy rzut oka mogą wydawać się, że nie są równi, więc być może będziemy musieli przyjrzeć się im bliżej!
Przykład: Czy A i B są równe, gdzie:
- A to zbiór, którego składnikami są pierwsze cztery dodatnie liczby całkowite
- B = {4, 2, 1, 3}
Sprawdźmy. Oba zawierają 1. Oba zawierają 2. I 3, I 4. Sprawdziliśmy każdy element obu zbiorów, więc: Tak, są równe!
I znak równości ( =) służy do pokazania równości, więc piszemy:
A = B

Podzbiory
Kiedy definiujemy zbiór, jeśli bierzemy części tego zbioru, możemy utworzyć tak zwany podzbiór.
Ogólnie:
A jest podzbiorem B wtedy i tylko wtedy, gdy każdy element A znajduje się w B.
Więc użyjmy tej definicji w kilku przykładach.
Spróbujmy trudniejszego przykładu.
Właściwe podzbiory
Jeśli spojrzymy na definicję podzbiorów i pozwolimy naszemu umysłowi błądzić, dochodzimy do dziwnego zakończenie.
Niech A będzie zbiorem. Czy każdy element A jest w A?
Cóż, hm, tak, oczywiście, prawda?
Oznacza to, że A jest podzbiorem A. Jest podzbiorem samego siebie!
To czy nie wydaje się być bardzo właściwe, prawda? Jeśli chcemy, aby nasze podzbiory były prawidłowe, wprowadzamy (co jeszcze) odpowiednie podzbiory:
A jest właściwym podzbiorem B wtedy i tylko wtedy, gdy każdy element A jest również w B i istnieje co najmniej jeden element w B, którego nie ma w A.
Ten mały fragment na końcu ma na celu upewnienie się, że A nie jest właściwy podzbiór samego siebie: mówimy, że B musi mieć co najmniej jeden dodatkowy element.
Przykład:
{1, 2, 3} jest podzbiorem {1, 2, 3}, ale nie jest odpowiednim podzbiorem {1, 2, 3}.
Przykład:
{1, 2, 3} jest właściwym podzbiorem {1, 2, 3, 4}, ponieważ element 4 nie znajduje się w pierwszym zestawie.
Zauważ, że kiedy A jest odpowiednim podzbiorem B, to jest również podzbiór B.
Jeszcze więcej notacji
Kiedy mówimy, że A jest podzbiorem B, piszemy A ![]() B.
B.
Albo my można powiedzieć, że A nie jest podzbiorem B przez A ![]() B („A nie jest podzbiorem B”)
B („A nie jest podzbiorem B”)
Kiedy mówimy o odpowiednich podzbiorach, usuwamy poniższą linię i staje się ona A ![]() B lub, jeśli chcemy powiedzieć coś przeciwnego, A
B lub, jeśli chcemy powiedzieć coś przeciwnego, A ![]() B.
B.
Pusty (lub zerowy) zestaw
To prawdopodobnie najdziwniejsza rzecz w zestawach.

Jako przykład pomyśl o zestawie klawiszy fortepianu na gitarze.
„Ale czekaj!”, mówisz: „Nie ma klawiszy fortepianu na gitara! ”
I masz rację. Jest to zbiór bez elementów.
Jest to znane jako zestaw pusty (lub zbiór zerowy). Nie ma w nim żadnych elementów. Ani jednego. Zero.
To jest reprezentowany przez ![]()
Lub przez {} (zbiór bez elementów)
Inne przykłady pustego zbioru to zbiór krajów na południe od bieguna południowego.
Więc co jest takiego dziwnego w tym pustym planie? Cóż, ta część jest następna.
Pusty zbiór i podzbiory
Więc wróćmy do naszej definicji podzbiorów. Mamy zbiór A. Nie będziemy go definiować co więcej, może to być dowolny zestaw. Czy pusty zbiór jest podzbiorem A?
Wracając do naszej definicji podzbiorów, jeśli każdy element w pustym zbiorze jest również w A, to pusty zbiór jest podzbiorem A. Ale co jeśli nie ma elementów?
Aby to zrozumieć, potrzeba wprowadzenia do logiki, ale to stwierdzenie jest „bezmyślnie” lub „trywialnie” prawdziwe.
Dobry sposób na przemyślenie to jest: nie możemy znaleźć żadnych elementów w pustym zbiorze, których nie ma w A, więc musi być tak, że wszystkie elementy w pustym zbiorze znajdują się w A.
A więc odpowiedź na postawione pytanie jest zdecydowanym tak.
Pusty zbiór to podzbiór każdego zestawu, w tym sam pusty zestaw.
Kolejność
Nie, nie kolejność elementów. W zestawach nie ma znaczenia, w jakiej kolejności znajdują się elementy.
Przykład: {1,2,3,4} to ten sam zbiór co {3,1,4,2}
Kiedy mówimy o kolejności w zestawach, mamy na myśli rozmiar zbioru.
Inną (lepszą) nazwą jest liczność.
Skończony zbiór ma skończony porządek (lub liczność). Nieskończony zbiór ma nieskończony porządek (lub liczność).
W przypadku skończonych zbiorów porządek (lub liczność) to liczba elementów.
Przykład: {10, 20, 30, 40} ma rząd 4.
W przypadku nieskończonych zbiorów jedyne, co możemy powiedzieć, to to, że kolejność jest nieskończona. Co dziwne, w przypadku zestawów możemy powiedzieć, że niektóre nieskończoności są większe niż inne, ale jest to bardziej zaawansowany temat dotyczący zestawów.
Arg! Nie więcej notacji!
Nie, tylko żartuję. Nigdy więcej notacji.
autorstwa
i