Hipoteza Poincarégo i 6 innych złożonych teorii matematycznych zostało nazwanych problemami nagrody milenijnej przez Clay Mathematics Institute (CMI). Każdy problem został opisany jako „ważne klasyczne pytanie, które przez lata opierało się rozwiązaniom”, przy czym pierwsza osoba, która dzięki uprzejmości CMI zarabia 1 000 000 dolarów, wymyśliła rozwiązanie. Jednak, jak widziałeś powyżej, rozwiązanie tych problemów nie jest łatwe feat. Jeden z problemów pozostał nierozwiązany od czasu sformułowania go w 1859 roku przez niemieckiego matematyka Bernharda Riemanna.
Hipoteza Riemanna, nazwana na cześć wspomnianego niemieckiego matematyka, jest powszechnie uważana za najważniejszy nierozwiązany problem w czystym matematyka. Jest bardzo interesująca w teorii liczb, ponieważ implikuje wyniki dotyczące rozkładu liczb pierwszych, które są używane we wszystkim, od biologii po szyfrowanie i mechanikę kwantową. Aby zrozumieć hipotezę Riemanna, najpierw musimy wyjaśnić kilka kluczowych pojęcia:
- Liczba zespolona ma postać a + bi, gdzie i jest zdefiniowane przez i² = -1. W tej postaci rzeczywistą częścią liczby zespolonej jest a, a urojoną część to bi.
- Funkcja zeta Riemanna jest funkcją zmiennej zespolonej (funkcji liczb zespolonych) zdefiniowanej przez następujące równanie, gdzie s jest dowolną liczbą zespoloną inną niż 1 i której wartości są również złożone:
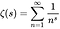
- „Zero” funkcji to taki x, że f (x) = 0
- Wszystkie „trywialne zera” funkcji zeta Riemanna to ujemne parzyste liczby całkowite (-2, -4, -6,…)
- „Nietrywialne zera ”Funkcji zeta Riemanna to wszystkie inne wartości s, dla których ζ (s) = 0 (tj. s nie jest ujemną liczbą parzystą).
Teraz, gdy mamy już pewne definicje, możemy przejść dalej i sformułować hipotezę Riemanna:
Rzeczywista część każdego nietrywialnego zera funkcji zeta Riemanna to 1/2
Ten (dla mnie przynajmniej) jest o wiele łatwiejsza do zrozumienia niż hipoteza Poincarégo i intuicyjnie nie wydaje się bardzo trudna. Jednak nie wydaje się to też wiele znaczyć. Naprawdę, kogo obchodzi, kiedy ta funkcja losowa ma wartość 0. Cóż, nie jest zaskakujące, że wielu matematyków to robi i nie bez powodu.
Niektóre liczby mają specjalną właściwość, której nie można wyrazić jako iloczyn dwóch mniejszych liczb (iloczyn jest mnożeniem), tj. 2,3,5,7,11 itd. Znane jako liczby pierwsze, są w pewnym sensie najprostszymi liczbami, jakie można uzyskać, tworząc bloki składowe wszystkich innych liczb. Frustrujące jest jednak to, że liczby pierwsze nie wydają się mieć żadnego wzoru. 3137 jest liczbą pierwszą, a następna po niej ma miejsce dopiero w 3163, ale potem następują po sobie 3167 i 3169, z których wszystkie są liczbami pierwszymi. Krótko mówiąc, jeśli znajdziesz jedną liczbę pierwszą, nie ma sposobu, aby stwierdzić, gdzie będzie następna, bez sprawdzania wszystkich liczb na bieżąco. Jednak korzystając z twierdzenia o liczbach pierwszych (PNT), możesz sprawdzić, ile liczb pierwszych jest poniżej określonego progu.
Twierdzenie o liczbach pierwszych to tylko oszacowanie, z różnymi wartościami dającymi różne prawdopodobieństwo bycia poprawne, ale nigdy 100% pewność. Jednakże, zrozum założenie, że hipoteza Reimanna jest prawdziwa, możesz stworzyć matematyczne przybliżenie łączące twierdzenie o liczbach pierwszych i nietrywialne zera funkcji zeta Riemanna, aby skorygować błędy składowych wewnętrznych, zapewniając „najlepsze możliwe” ograniczenie dla składnik błędu w twierdzeniu o liczbach pierwszych. Gdyby możliwe było całkowite udowodnienie hipotezy Reimanna, dałoby to PNT zdolność do dostarczania niewiarygodnie dokładnych szacunków wartości rzeczywistej, otwierając wiele możliwości w różnych gałęziach matematyki. istnieje wiele ważnych hipotez, że bycie z „Jeśli hipoteza Riemanna jest prawdziwa, to …”, więc rozwiązanie tego problemu natychmiast potwierdziłoby również wszystkie późniejsze przypuszczenia.