Was ist Standardabweichung? | STDEV.P | STDEV.S | Varianz
Auf dieser Seite wird erläutert, wie Sie die Standardabweichung basierend auf der gesamten Grundgesamtheit mithilfe der STDEV.P-Funktion in Excel berechnen und die Standardabweichung basierend auf einer Stichprobe mithilfe der STDEV.S-Funktion in Excel schätzen.
Was ist Standardabweichung?
Standardabweichung ist eine Zahl, die angibt, wie weit Zahlen von ihrem Mittelwert entfernt sind.
1. Zum Beispiel haben die folgenden Zahlen einen Mittelwert (Durchschnitt) von 10.
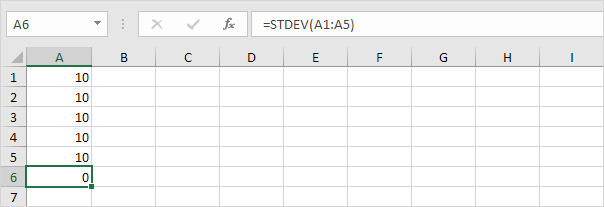
Erläuterung: Die Zahlen sind alle gleich bedeutet, dass es keine Abweichungen gibt. Daher haben die Zahlen eine Standardabweichung von Null. Die STDEV-Funktion ist eine alte Funktion. Microsoft Excel empfiehlt die Verwendung der neuen STEDV.S-Funktion, die genau das gleiche Ergebnis liefert.
2. Die folgenden Zahlen haben auch einen Mittelwert (Durchschnitt) von 10.
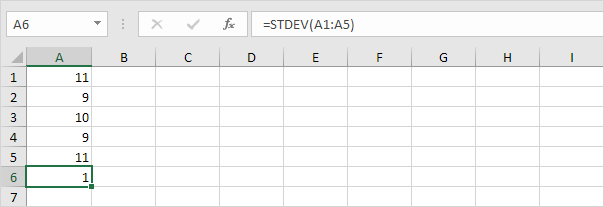
Erläuterung: Die Zahlen liegen nahe am Mittelwert. Infolgedessen weisen die Zahlen eine geringe Standardabweichung auf.
3. Die folgenden Zahlen haben auch einen Mittelwert (Durchschnitt) von 10.
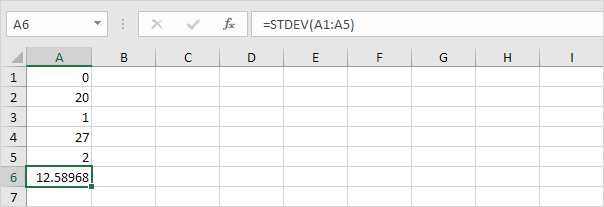
Erläuterung: Die Zahlen sind verteilt. Infolgedessen weisen die Zahlen eine hohe Standardabweichung auf.
STDEV.P
Die STDEV.P-Funktion (das P steht für Population) in Excel berechnet die Standardabweichung basierend auf der gesamten Population. Sie unterrichten beispielsweise eine Gruppe von 5 Schülern. Sie haben die Testergebnisse aller Schüler. Die gesamte Bevölkerung besteht aus 5 Datenpunkten. Die STDEV.P-Funktion verwendet die folgende Formel:
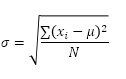
In diesem Beispiel ist x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (Mittelwert), N = 5 (Anzahl der Datenpunkte).
1. Berechnen Sie den Mittelwert (μ).
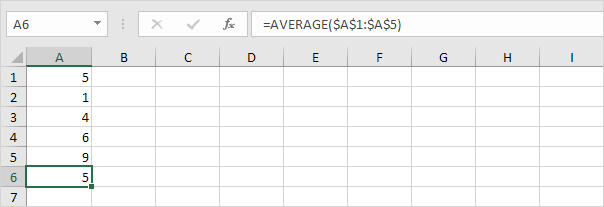
2. Berechnen Sie für jede Zahl den Abstand zum Mittelwert.
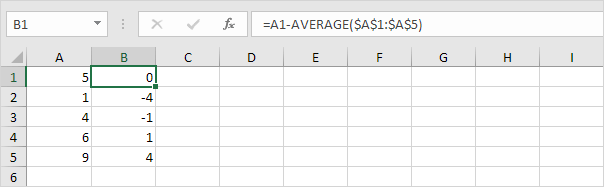
3. Quadrieren Sie für jede Zahl diesen Abstand.
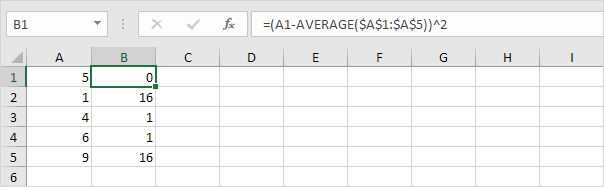
4. Summieren Sie diese Werte (∑).
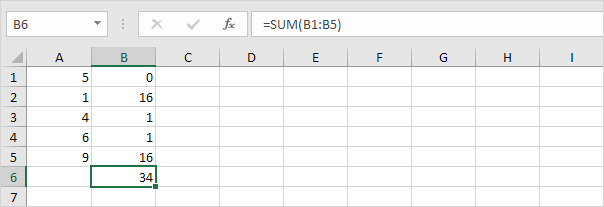
5. Teilen Sie durch die Anzahl der Datenpunkte (N = 5).
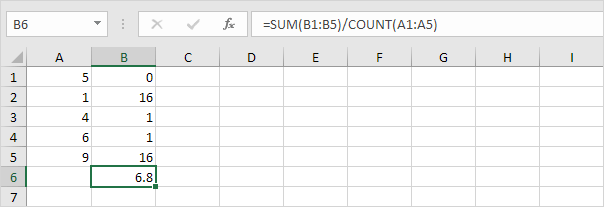
6. Nehmen Sie die Quadratwurzel.
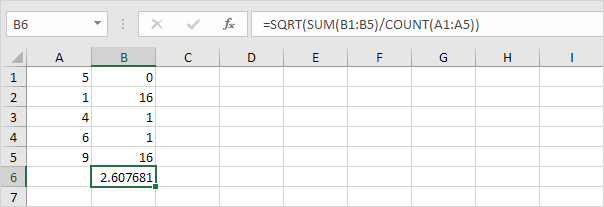
7. Glücklicherweise kann die STDEV.P-Funktion in Excel alle diese Schritte für Sie ausführen.
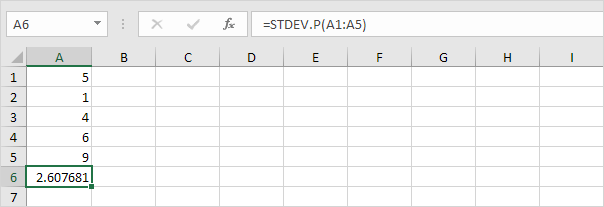
STDEV.S
Die STDEV.S-Funktion (das S steht für Sample) in Excel schätzt die Standardabweichung basierend auf einem Sample. Zum Beispiel unterrichten Sie eine große Gruppe von Schülern. Sie haben nur die Testergebnisse von 5 Schülern. Die Stichprobengröße beträgt 5. Die STDEV.S-Funktion verwendet die folgende Formel:
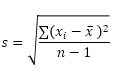
In diesem Beispiel ist x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (gleiche Zahlen wie oben), x̄ = 5 (Probe) Mittelwert), n = 5 (Stichprobengröße).
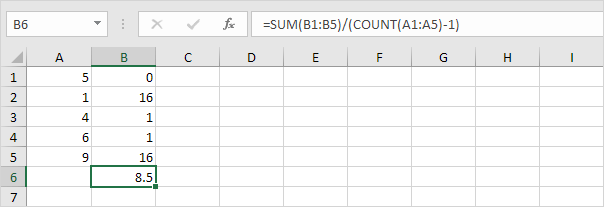
1. Wiederholen Sie die obigen Schritte 1 bis 5, aber teilen Sie in Schritt 5 durch n-1 anstelle von N.
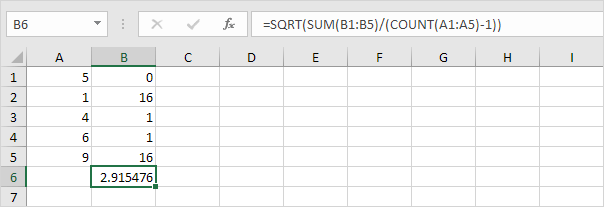
2. Nehmen Sie die Quadratwurzel.
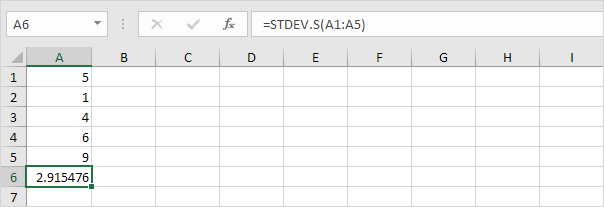
3. Glücklicherweise kann die STDEV.S-Funktion in Excel alle diese Schritte für Sie ausführen.
Hinweis: Warum teilen wir durch n – 1 statt durch n, wenn wir die Standardabweichung basierend auf einer Stichprobe schätzen? Bessels Korrektur besagt, dass die Division durch n-1 anstelle von n eine bessere Schätzung der Standardabweichung ergibt.
Varianz
Varianz ist das Quadrat der Standardabweichung. So einfach ist das. Manchmal ist es einfacher, die Varianz bei der Lösung statistischer Probleme zu verwenden.
1. Die folgende VAR.P-Funktion berechnet die Varianz basierend auf der gesamten Grundgesamtheit.
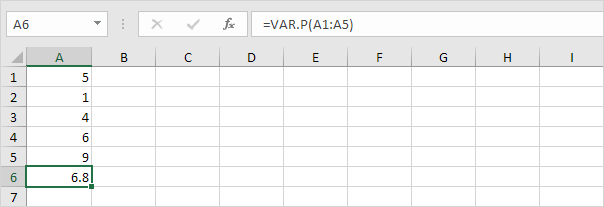
Hinweis: Sie kannten diese Antwort bereits (siehe Schritt 5 unter STDEV.P). Verwenden Sie die Quadratwurzel dieses Ergebnisses, um die Standardabweichung basierend auf der gesamten Grundgesamtheit zu ermitteln.
2. Die folgende VAR.S-Funktion schätzt die Varianz anhand einer Stichprobe.
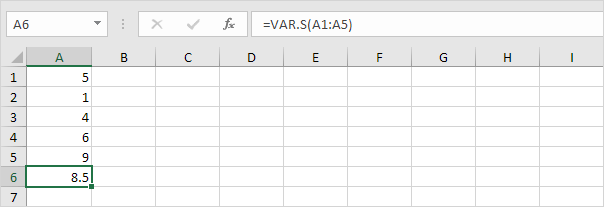
Hinweis: Sie kannten diese Antwort bereits (siehe Schritt) 1 unter STDEV.S). Verwenden Sie die Quadratwurzel dieses Ergebnisses, um die Standardabweichung basierend auf einer Stichprobe zu ermitteln.
3. VAR und VAR.S liefern genau das gleiche Ergebnis.
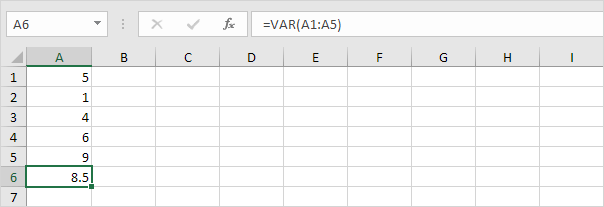
Hinweis: Microsoft Excel empfiehlt die Verwendung der neuen VAR.S-Funktion.