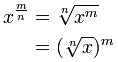Även kallade ”Radikaler” eller ”Rationella exponenter”
Hela antalet exponenter
Låt oss först titta på heltal exponenter:

Exponenten för ett tal säger hur många gånger numret ska användas i en multiplikation.
I det här exemplet: 82 = 8 × 8 = 64
Ett annat exempel: 53 = 5 × 5 × 5 = 125
Fraktionerade exponenter
Men tänk om exponenten är en bråkdel?
|
En exponent på 12 är faktiskt kvadratrot En exponent på 13 är kubrot En exponent av 14 är fjärde roten Och så vidare! |
 |
Varför?
Låt oss se varför i en exempel.
Först berättar lagen om exponenter hur vi ska hantera exponenter när vi multiplicerar:
Exempel: x2x2 = (xx) (xx) = xxxx = x4
Som visar att x2x2 = x (2 + 2) = x4
Så låt oss prova det med fraktionerade exponenter:
Prova en annan bråkdel
Låt oss försöka igen, men med en exponent på en fjärdedel (1/4):
Exempel:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Så 16¼ som används 4 gånger i en multiplikation ger 16,
och så är 16¼ en Fjärde roten av 16
Allmän regel
Det fungerade för ½, det fungerade med ¼, faktiskt fungerar det generellt:
x1 / n = Den n: te roten till x
Så vi kan komma på det här:
| |
|
Exempel: Vad är 271/3?
Svar: 271/3 = ![]() 27 = 3
27 = 3
Vad sägs om mer komplicerade fraktioner?
Vad sägs om en fraktionerad exponent som 43/2?
Det är verkligen att säga att göra en kub (3) och en kvadratrot (1/2), i vilken ordning som helst.
Låt mig förklara.
En bråkdel (som m / n) kan delas upp i två delar:
- en heltaldel (m) och
- en bråkdel (1 / n) del
Så eftersom m / n = m × (1 / n) kan vi göra detta:
Ordningen spelar ingen roll, så det fungerar också för m / n = (1 / n) × m:
Och vi får detta:
| |
|
Några exempel:
Exempel : Vad är 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
eller
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
Hur som helst får samma resultat.
Exempel: Vad är 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
eller
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
Det var verkligen lättare den andra vägen!
Nu … Spela med diagrammet!
Se hur smidigt kurvan ändras när du spelar med bråk i den här animationen, detta visar dig att denna idé om fraktionerade exponenter passar bra ihop:
Saker att prova:
- Börja med m = 1 och n = 1, öka sedan långsamt n så att du kan se 1/2, 1/3 och 1/4
- Testa sedan m = 2 och skjut n uppåt och nedåt för att se bråk som 2/3 etc
- Försök nu göra exponenten -1
- Slutligen försök att öka m, sedan minska n, sedan minska m, sedan öka n: kurvan ska gå runt och runt