Glöm allt du vet om siffror.
Glöm faktiskt att du ens vet vad ett nummer är.
Detta där matematik börjar.
I stället för matematik med siffror kommer vi nu att tänka på matematik med ”saker”.
Definition
Vad är en uppsättning? Tja, helt enkelt, det är en samling.
Först anger vi en gemensam egenskap bland ”saker” (vi definierar detta ord senare) och sedan samlar vi alla ”saker” som har denna gemensamma egendom.

Till exempel de saker du bär: hatt, skjorta, jacka, byxor och så vidare.
Jag är säker på att du kan komma med minst hundra.
Detta kallas en uppsättning.
|
Eller ett annat exempel är typer av fingrar. Denna uppsättning innehåller index, mitt, ring och pinky. |
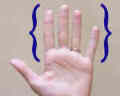 |
Så det är bara saker grupperade tillsammans med en viss egenskap gemensamt.
Notation
Det finns en ganska enkel notation för uppsättningar. Vi listar helt enkelt varje element (eller ”medlem”) åtskilt med ett komma och lägger sedan några lockiga parenteser runt det hela:

De lockiga parenteserna {} kallas ibland ”set parentes” eller ”parenteser”.
Detta är notationen för de två föregående exemplen:
{strumpor, skor, klockor, skjortor, …}
{index, mitt, ring, rosa}
Lägg märke till hur det första exemplet har ”…” (tre punkter tillsammans) .
De tre punkterna … kallas en ellips och betyder ”fortsätt”.
Så det betyder att det första exemplet fortsätter … för oändlighet.
(OK, det finns inte en oändlig mängd saker du kan ha på dig, men jag är inte helt säker på det! Efter en timmes tänkande på olika saker, jag ”m fortfarande inte säker. Så låt oss bara säga att det är oändligt för det här exemplet.)
Så:
Men ibland kan ”…” användas i mitten för att spara skriva långa listor:
Exempel: uppsättningen bokstäver:
{a, b, c, .. ., x, y, z}
I det här fallet är det en ändlig uppsättning (det finns bara 26 bokstäver, eller hur?)
Numeriska uppsättningar
Så vad har detta med matematik att göra? När vi definierar en uppsättning är allt vi behöver ange en gemensam egenskap. Vem säger att vi inte kan göra det med siffror?
Och så vidare. Vi kan komma på alla olika typer av uppsättningar.
Vi kan också definiera en uppsättning med dess egenskaper, såsom {x | x > 0} vilket betyder ”uppsättningen av alla x”, så att x är större än 0 ”, se Set-Builder Notation för att lära dig mer.
Och vi kan ha uppsättningar med siffror som inte har någon gemensam egenskap, de definieras bara på det sättet. Till exempel:
{4, 5, 6, 10, 21}
{2, 949, 48282, 42882959, 119484203 }
Är alla uppsättningar som jag slumpmässigt slog på mitt tangentbord för att producera.
Varför är uppsättningar viktiga?
Uppsättningar är matematikens grundläggande egenskap. Nu som ett varningsord verkar uppsättningar i sig ganska meningslösa. Men det är bara när vi använder uppsättningar i olika situationer, de blir den kraftfulla byggstenen för matematik som de är.
Matematik kan bli otroligt komplicerad ganska snabbt. Grafteori, abstrakt algebra, verklig analys, komplex Analys, linjär algebra, talteori och listan fortsätter. Men det är en sak som alla dessa har gemensamt: uppsättningar.
Universaluppsättning
 |
I början använde vi ordet ”saker” i citat. Vi kallar detta den universella uppsättningen. Den är en uppsättning som innehåller allt. Tja, inte precis allt. Allt som är relevant för vår fråga. |
|
 |
I Number Theory är den universella uppsättningen alla heltal, eftersom Number Theory helt enkelt är studie av heltal. |
|
 |
Men i Calculus (även känd som verklig analys) är den universella uppsättningen nästan alltid de verkliga siffrorna. |
|
 |
Och i komplex analys gissade du det, den universella uppsättningen är de komplexa siffrorna. |
Lite mer notering
 |
När vi talar om uppsättningar är det ganska standard att använda versaler och små bokstäver för att representera ett element i den uppsättningen. Så till exempel är A en uppsättning och a är ett element nt i A. Samma med B och b, och C och c. |
Nu behöver du inte lyssna på standarden , du kan använda något som m för att representera en uppsättning utan att bryta några matematiska lagar (se upp, du kan få π år i matematikfängelse för att dela med 0), men denna notation är ganska trevlig och lätt att följa, så varför inte? / p>
När vi säger att ett element a är i en uppsättning A använder vi symbolen ![]() för att visa det.
för att visa det.
Och om något inte finns i en set använd ![]() .
.
Exempel: Set A är {1,2,3}. Vi kan se att 1 ![]() A, men 5
A, men 5 ![]() A
A
Jämställdhet
Två uppsättningar är lika om de har exakt samma medlemmar. Nu vid första anblicken kanske de inte verkar lika, så vi kan behöva undersöka dem noggrant!
Exempel: Är A och B lika där:
- A är den uppsättning vars medlemmar är de första fyra positiva heltalen
- B = {4, 2, 1, 3}
Låt oss kontrollera. De innehåller båda 1. De innehåller båda 2. Och 3, Och 4. Och vi har kontrollerat alla element i båda uppsättningarna, så: Ja, de är lika!
Och likhetstecknet ( =) används för att visa jämlikhet, så vi skriver:
A = B

Delmängder
När vi definierar en uppsättning, om vi tar bitar av den uppsättningen, kan vi bilda det som kallas en delmängd.
I allmänhet:
A är en delmängd av B om och bara om varje element i A finns i B.
Så låt oss använda denna definition i några exempel.
Låt oss försöka ett hårdare exempel.
Korrekta underuppsättningar
Om vi tittar på definitionen av underuppsättningar och låter vårt sinne vandra lite, kommer vi till en konstig slutsats.
Låt A vara en uppsättning. Finns varje element i A i A?
Tja, umm, ja naturligtvis, eller hur?
Så det betyder att A är en delmängd av A. Det är en delmängd av sig själv!
Detta verkar inte riktigt riktigt, eller hur? Om vi vill att våra underuppsättningar ska vara korrekta introducerar vi (vad annat än) rätt underuppsättningar:
A är en ordentlig delmängd av B om och bara om varje element av A finns också i B, och det finns minst ett element i B som inte finns i A.
Denna lilla bit i slutet finns för att se till att A inte är en rätt delmängd av sig själv: vi säger att B måste ha minst ett extra element.
Exempel:
{1, 2, 3} är en delmängd av {1, 2, 3}, men är inte en riktig delmängd av {1, 2, 3}.
Exempel:
{1, 2, 3} är en riktig delmängd av {1, 2, 3, 4} eftersom elementet 4 inte finns i den första uppsättningen.
Observera att när A är en riktig delmängd av B så är det också en delmängd av B.
Ännu mer notering
När vi säger att A är en delmängd av B, skriver vi A ![]() B.
B.
Eller vi kan säga att A inte är en delmängd av B av A ![]() B (”A är inte en delmängd av B”)
B (”A är inte en delmängd av B”)
När vi pratar om rätt delmängder, vi tar ut raden under och så blir det A ![]() B eller om vi vill säga det motsatta, A
B eller om vi vill säga det motsatta, A ![]() B.
B.
Tom (eller noll) Set
Detta är förmodligen det konstigaste med uppsättningar.

Tänk som exempel på uppsättningen pianotangenter på en gitarr.
”Men vänta!” du säger, ”Det finns inga pianotangenter på en gitarr! ”
Och du har rätt. Det är en uppsättning utan element.
Detta är känt som den tomma uppsättningen (eller nolluppsättningen). Det finns inga element i den. Inte en. Noll.
Det är representeras av ![]()
Eller av {} (en uppsättning utan element)
Några andra exempel på den tomma uppsättningen är uppsättningen av länder söder om sydpolen.
Så vad är så konstigt med den tomma uppsättningen? Den delen kommer därefter.
Tom uppsättning och delmängder
Så låt oss gå tillbaka till vår definition av delmängder. Vi har en uppsättning A. Vi kommer inte att definiera den någon mer än så kan det vara vilken uppsättning som helst. Är den tomma uppsättningen en delmängd av A?
Återgår vi till vår definition av delmängder, om varje element i den tomma uppsättningen också är i A, är den tomma uppsättningen en delmängd av A. Men vad händer om vi har inga element?
Det krävs en introduktion till logiken för att förstå detta, men detta uttalande är ett som är ”vakuum” eller ”triviellt” sant.
Ett bra sätt att tänka på det är: vi kan inte hitta några element i den tomma uppsättningen som inte finns i A, så det måste vara så att alla element i den tomma uppsättningen finns i A.
Så svaret på den ställda frågan är ett rungande ja.
Den tomma uppsättningen är en delmängd av varje uppsättning, inklusive själva den tomma uppsättningen.
Beställning
Nej, inte elementens ordning. I uppsättningar spelar det ingen roll i vilken ordning elementen är.
Exempel: {1,2,3,4} är samma uppsättning som {3,1,4,2}
När vi säger ordning i uppsättningar menar vi storleken på uppsättningen.
Ett annat (bättre) namn för detta är kardinaliteten.
En ändlig uppsättning har ändlig ordning (eller kardinalitet). En oändlig uppsättning har oändlig ordning (eller kardinalitet).
För ändliga uppsättningar är ordningen (eller kardinaliteten) antalet element.
Exempel: {10, 20, 30, 40} har ordningen 4.
För oändliga uppsättningar kan vi bara säga att ordningen är oändlig. Konstigt nog kan vi säga med uppsättningar att vissa oändligheter är större än andra, men detta är ett mer avancerat ämne i uppsättningar.
Arg! Inte mer notation!
Nej, bara skojar. Inget mer notation.
av
och