Kostnadsvolym-vinstanalys

Cost-Volume-Profit (CVP) analys är en ledningsredovisningsteknik som studerar effekten av försäljningsvolym och produktkostnader på ett företags rörelseresultat. Den visar hur rörelseresultatet påverkas av förändringar i rörliga kostnader, fasta kostnader, försäljningspris per enhet och försäljningsmix av två eller flera produkter.

CVP-analys handlar om identifiering av företagets fasta kostnader , dess rörliga kostnad per enhet, priset på sin produkt och att använda dessa data för att ta fram följande mått:

• Avgiftsmarginal: Skillnaden mellan företagets totala intäkter och de totala rörliga kostnaderna. Det är det belopp som försäljningen bidrar till fasta kostnader och vinst.
• Avgiftsmarginal per enhet: Skillnaden mellan försäljningspris och rörlig kostnad per enhet.
• Avgiftsmarginal: förhållandet mellan bidragsmarginal till totala intäkter.
• Break-even point: Försäljningsvolymen (i enheter och dollar) där företaget varken gör förlust eller tjänar någon vinst.
• Målintäktsförsäljning: Den nödvändiga försäljningsnivån för att uppnå en målinkomst.
• Säkerhetsmarginal: Procentandelen (eller dollar) som ett företags försäljningsvolym överstiger dess break-even-punkt.

den mest kritiska insatsen i CVP-analysen är förhållandet mellan olika kostnader och volym, dvs kategorisering av kostnader i fasta och variabla kategorier.

CVP-analysekvation

Det grundläggande förhållandet mellan kostnad och volym-vinst kan härledas från vinstekvationen:

Vinst = Intäkter – Fasta kostnader – Variabla kostnader

Om vinsten är PR, motsvarar intäkterna produkten av pris per enhet P och försäljningsvolym i enheter Q , fasta kostnader FC är konstanta och totala rörliga kostnader motsvarar produkten av sålda enheter Q och rörlig kostnad per enhet V, följande ekvation är en mer detaljerad representation av CVP-förhållanden:

PR = Q × P – Q × V – FC

Detta är den mest grundläggande ekvationen som kan användas för att arbeta många CVP-nummer.

För paus -och punkt måste vi ställa in PR-annons 0 och lösa för Q och vi får:

Break-even Q = FC ÷ (P – V)

Det visar att break- jämn poäng kan beräknas genom att dela fast kostnad med avgiftsmarginalen per enhet.

Tillvägagångssätt för marginalekvation

CVP-ekvationen som diskuterats ovan kan också uttryckas i termer av bidragsmarginalen för produkt:

PR = Q × P – Q × V – FC

PR = Q × (P – V) – FC

(P – V) i ekvationen ovan är avgiftsmarginal per enhet.

CVP-diagram

CVP-förhållande kan också uttryckas i form av ett diagram som kallas CVP-diagram:

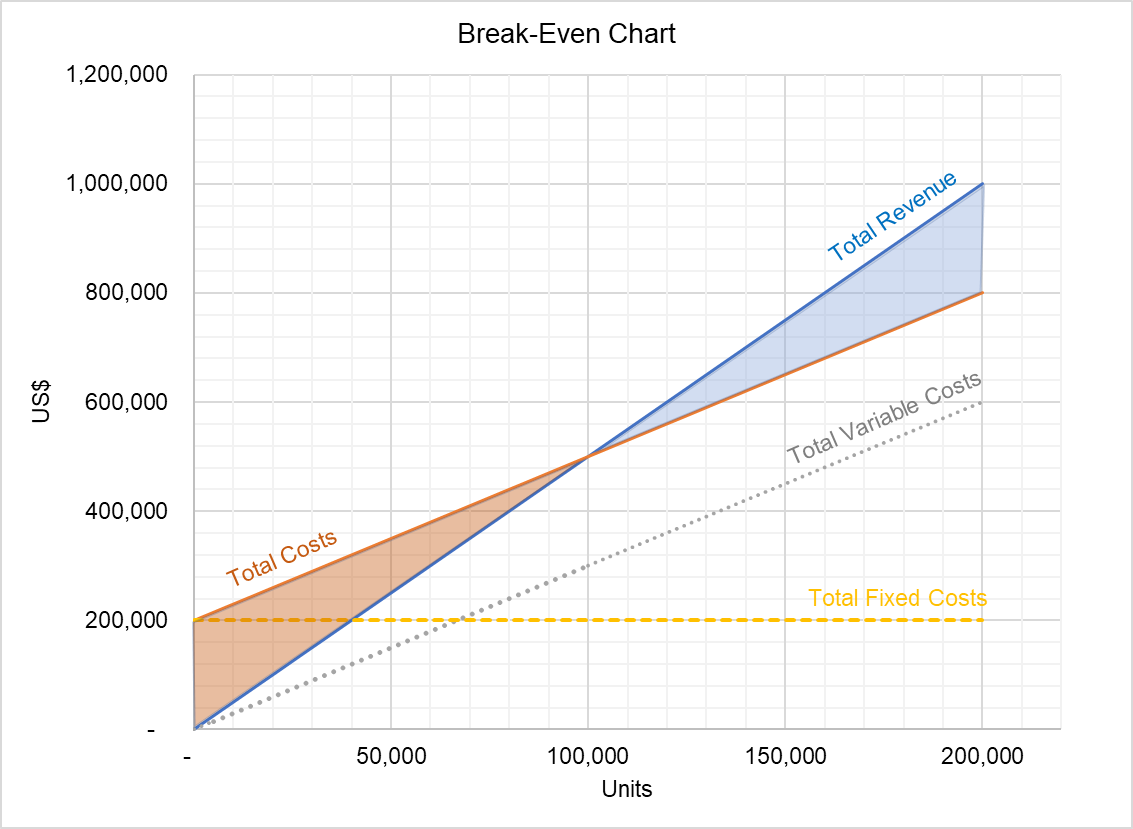
Diagrammet ovan visar sambandet mellan totala intäkter och totala kostnader. Området mellan de två raderna under break-even-punkten representerar förluster och området över break-even-punkten visar volymen av den totala vinsten. Denna graf kan användas för att identifiera vinst vid olika utgångsnivåer.

Antaganden om CVP-analys

Även om CVP-analys är ett användbart redovisningsverktyg är dess slutsatser giltiga endast när följande antaganden håll:

• Alla kostnader kan kategoriseras som variabla eller fasta. För detta ändamål delas blandade kostnader in i variabla och fasta komponenter med tekniker såsom hög-låg-metod, spridningsgrafmetod och regressionsanalys.
• Försäljningspris per enhet, rörlig kostnad per enhet och total fast kostnad är konstant . Detta antagande är problematiskt på grund av att det finns skalfördelar, ökande / minskande skalavkastning och inlärningskurvan.
• Alla intäkter och kostnader har en linjär relation till volymen.
• Försäljningen en blandning av ett företag förblir konstant.

av Irfanullah Jan, ACCA och senast ändrad den 2 oktober 2020