Vad är standardavvikelse? | STDEV.P | STDEV.S | Varians
Den här sidan förklarar hur man beräknar standardavvikelsen baserat på hela populationen med STDEV.P-funktionen i Excel och hur man uppskattar standardavvikelsen baserat på ett prov med STDEV.S-funktionen i Excel.
Vad är standardavvikelse?
Standardavvikelse är ett tal som berättar hur långt tal är från deras medelvärde.
1. Till exempel har siffrorna nedan ett medelvärde (medelvärde) på 10.
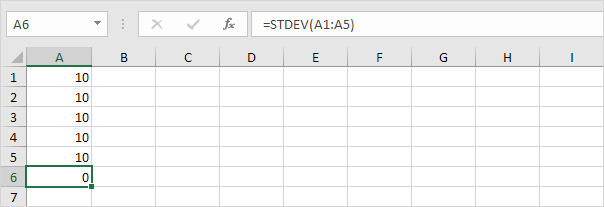
Förklaring: siffrorna är alla desamma som betyder att det inte finns någon variation. Som ett resultat har siffrorna en standardavvikelse på noll. STDEV-funktionen är en gammal funktion. Microsoft Excel rekommenderar att du använder den nya STEDV.S-funktionen som ger exakt samma resultat.
2. Siffrorna nedan har också ett medelvärde (genomsnitt) på 10.
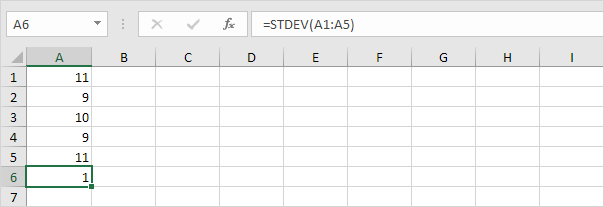
Förklaring: siffrorna ligger nära medelvärdet. Som ett resultat har siffrorna en låg standardavvikelse.
3. Siffrorna nedan har också ett medelvärde (medelvärde) på 10.
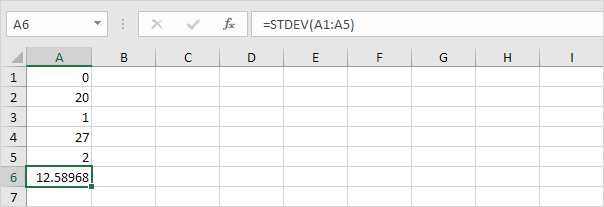
Förklaring: siffrorna är utspridda. Som ett resultat har siffrorna en hög standardavvikelse.
STDEV.P
STDEV.P-funktionen (P står för Population) i Excel beräknar standardavvikelsen baserat på hela befolkningen. Du lär till exempel ut en grupp på 5 elever. Du har testresultaten för alla studenter. Hela befolkningen består av 5 datapunkter. STDEV.P-funktionen använder följande formel:
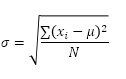
I detta exempel är x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (medelvärde), N = 5 (antal datapunkter).
1. Beräkna medelvärdet (μ).
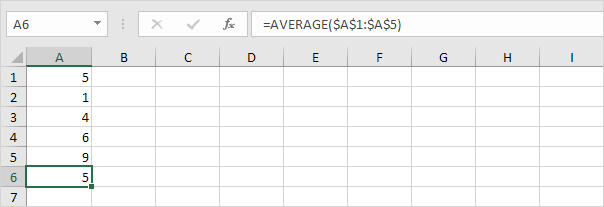
2. Beräkna avståndet till genomsnittet för varje nummer.
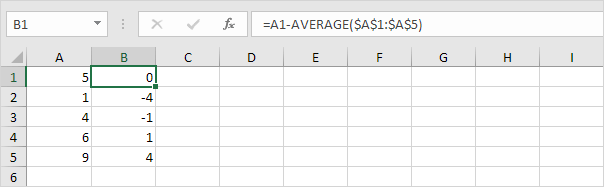
3. Kvadrera detta avstånd för varje nummer.
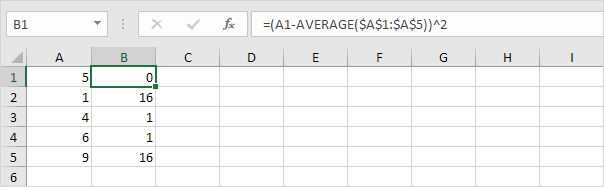
4. Summa (∑) dessa värden.
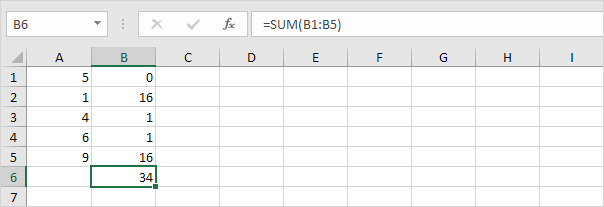
5. Dela med antalet datapunkter (N = 5).
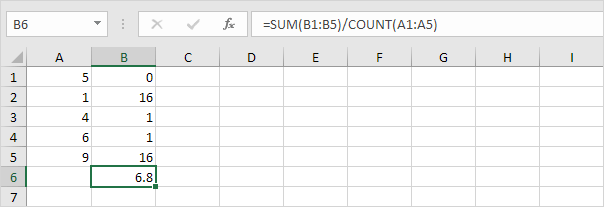
6. Ta kvadratroten.
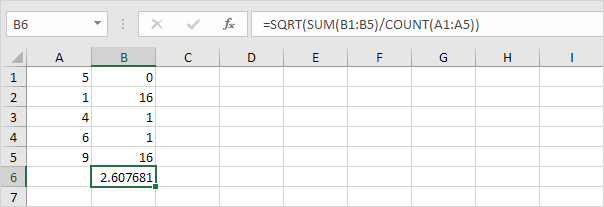
7. Lyckligtvis kan STDEV.P-funktionen i Excel utföra alla dessa steg åt dig.
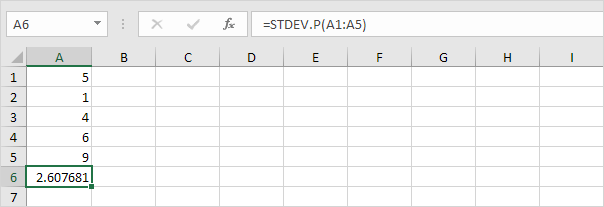
STDEV.S
STDEV.S-funktionen (S står för Sample) i Excel uppskattar standardavvikelsen baserat på ett urval. Till exempel undervisar du en stor grupp elever. Du har bara testpoängen på 5 elever. Provstorleken är lika med 5. STDEV.S-funktionen använder följande formel:
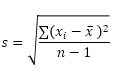
I detta exempel är x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (samma siffror som ovan), x̄ = 5 (exempel medelvärde), n = 5 (provstorlek).
1. Upprepa steg 1-5 ovan men vid steg 5 dividera med n-1 istället för N.
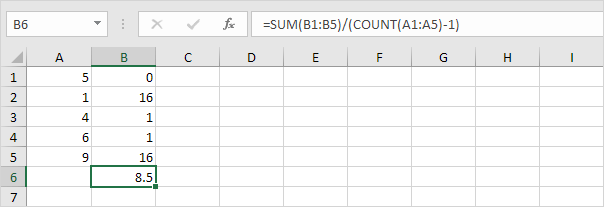
2. Ta kvadratroten.
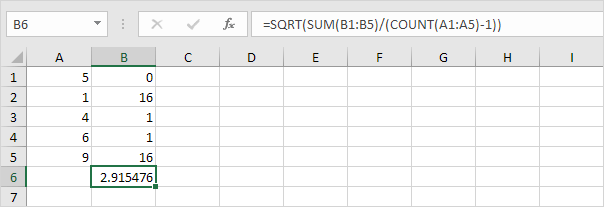
3. Lyckligtvis kan STDEV.S-funktionen i Excel utföra alla dessa steg åt dig.
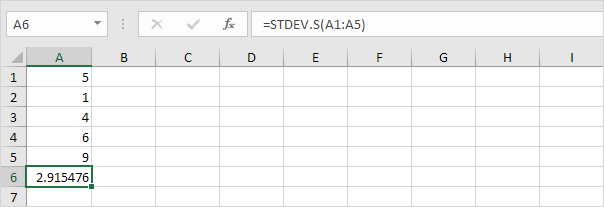
Obs: varför delar vi med n – 1 istället för med n när vi uppskattar standardavvikelsen baserat på ett urval? Bessels korrigering säger att att dividera med n-1 istället för med n ger en bättre uppskattning av standardavvikelsen.
Varians är kvadraten för standardavvikelsen. Det är så enkelt. Ibland är det lättare att använda variansen när man löser statistiska problem.
1. VAR.P-funktionen nedan beräknar variansen baserat på hela befolkningen.
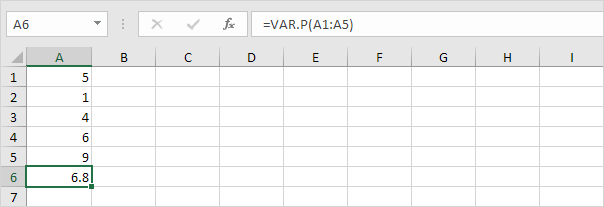
Obs! Du visste redan detta svar (se steg 5 under STDEV.P). Ta kvadratroten av detta resultat för att hitta standardavvikelsen baserat på hela befolkningen.
2. VAR.S-funktionen nedan uppskattar variansen baserat på ett prov.
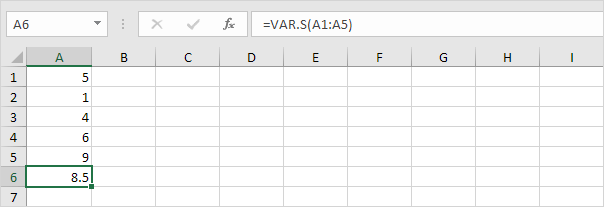
Obs! Du visste redan detta svar (se steg 1 under STDEV.S). Ta kvadratroten av detta resultat för att hitta standardavvikelsen baserat på ett exempel.
3. VAR och VAR.S ger exakt samma resultat.
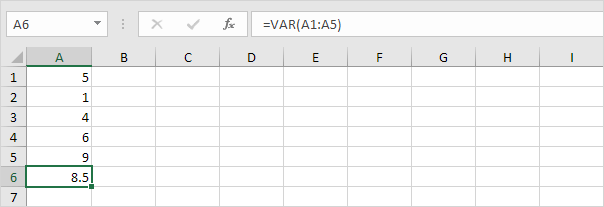
Obs! Microsoft Excel rekommenderar att du använder den nya VAR.S-funktionen.