Poincaré-antagandet och 6 andra komplexa matematiska teorier har kallats Millennium Prize Problems av Clay Mathematics Institute (CMI). Varje problem har beskrivits som en ”viktig klassisk fråga som har motstått lösningar genom åren”, med den första personen som utarbetade en lösning för var och en att tjäna $ 1 000 000 med tillstånd av CMI. Men som ni såg ovan är det inte lätt att lösa dessa problem. feat. Ett av problemen har förblivit olöst sedan den formulerades 1859 av den tyska matematikern Bernhard Riemann.
Riemann-hypotesen, uppkallad efter den tidigare nämnda tyska matematikern, anses allmänt vara det viktigaste olösta problemet i ren matematik. Det är av stort intresse för talteori eftersom det innebär resultat om fördelningen av primtal, som används i allt från biologi till kryptering och kvantmekanik. För att förstå Riemann-hypotesen måste vi först förklara några viktiga begrepp:
- Ett komplext tal har formen a + bi, där i definieras av i² = -1. I denna form är den verkliga delen av ett komplext tal a, och det imaginära del är bi.
- Riemann zeta-funktionen är en funktion av en komplex variabel (en funktion av komplexa tal) definierad av följande ekvation, där s är något annat komplex än 1, och vars värden också är komplexa:
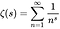
- En ”noll” för en funktion är ett x så att f (x) = 0
- De ”triviala nollorna” i Riemann zeta-funktionen är alla negativa jämna heltal (-2, -4, -6,…)
- De ”icke-triviala nollorna ”I Riemann zeta-funktionen är alla andra värden på s för vilka ζ (s) = 0 (dvs. s är inte ett negativt jämnt heltal).
Nu när vi har några definitioner nere, kan vi gå vidare och ange Riemann-hypotesen:
Den verkliga delen av varje icke-trivial nolla i Riemann zeta-funktionen är 1/2
Den här (för mig åtminstone) är mycket lättare att förstå än Poincaré-antagandet och verkar inte intuitivt särskilt svårt. Men det verkar inte heller betyda mycket. Verkligen vem bryr sig om när denna slumpmässiga funktion har värdet 0. Det är inte förvånande att många matematiker gör det, och av en mycket god anledning.
Vissa siffror har den speciella egenskapen att de inte kan uttryckas som produkten av två mindre antal (produkten multipliceras), dvs. 2,3,5,7,11, etc. Kända som primtal, de är på sätt och vis de enklaste siffrorna du kan få och bildar byggstenarna för alla andra siffror. Frustrerande dock verkar primtal inte följa något mönster. 3137 är ett primtal, och nästa efter det är inte förrän 3163, men sedan följer 3167 och 3169 i snabb följd, som alla är primtal. Kort sagt, om du hittar ett primtal, finns det inget sätt att berätta var nästa kommer att vara utan att kontrollera alla siffror när du går. Med hjälp av Prime Number Theorem (PNT) kan du hitta hur många primtal som finns under en viss tröskel.
Prime Number Theorem är bara en uppskattning, med olika värden som ger en annan sannolikhet att vara korrekt, men aldrig 100% säkerhet. Förstå dock antagandet att Reimann-hypotesen är sant, du kan skapa en matematisk approximation som kombinerar primtalstalet och de icke-triviala nollorna i Riemann zeta-funktionen för att felkorrigera de interna komponenterna, vilket ger ”bästa möjliga” gräns för feluttrycket i Prime Number Theorem. Om det vore möjligt att bevisa Reimann-hypotesen helt, skulle detta ge PNT möjligheten att ge otroligt nära uppskattningar till det verkliga värdet, vilket öppnar många möjligheter inom olika grenar av matematik. det finns många viktiga hypoteser att vara med ”Om Riemann-hypotesen är sant, då …”, så att lösa detta problem skulle också omedelbart validera alla efterföljande antaganden.