Kinematiska data för båda afrikanska arterna var svåra att hitta, men ladan eller den europeiska svalan (Hirundo rustica) har studerats intensivt och kinematisk för den arten var lätt tillgänglig.
Det är en enkel fråga om viktförhållanden
En 54-årig undersökning av 26 285 europeiska svalor fångade och släpptes av Avian Demography Unit of the University of Capetown finner att den genomsnittliga vuxna europeiska svalen har en vinglängd på 12,2 cm och en kroppsmassa på 20,3 gram. 4 uppgifter finns tillgängliga för minst 22 andra fågelarter, 6 bör det vara möjligt att uppskatta frekvensen (f) och amplituden (A) för den europeiska svalan genom en jämförelse med liknande arter. Med dessa två siffror är det möjligt att uppskatta lufthastighet (U).
För att upprätthålla lufthastighetshastigheten måste en svala slå sina vingar fyrtiotre gånger varje sekund, eller hur?
Egentligen fel. Genom att jämföra den europeiska svalan med fågelarter med liknande kroppsmassa kan vi uppskatta att svalan slår sina vingar 18 gånger per sekund med en amplitud på 18 cm:
| Arter | Kroppsmassa | Frekvens | Amplitud |
| Zebrafink | 13 g | 27 Hz | 11 cm |
| European Swallow | 20 g | ≈ 18 Hz? | ≈ 18 cm? |
| Dunig hackspett | 27 g | 14 Hz | 29 cm |
| Undulat | 34 g | 14 Hz | 15 cm |
Observera att även den lilla zebrafinken klappar vingarna inte mer än 27 gånger per sekund när vi kryssar.
Om vi ignorerar kroppsmassa och bara ser på fågel sp ecies med liknande vingbredd kan vi uppskatta en genomsnittlig frekvens på 14 slag per sekund och en amplitud på 23 cm:
| Arter | Vingspanel | Frekvens | Amplitude |
| Budgerigar | 27 cm | 14 Hz | 15 cm |
| European Swallow | ≈ 28–30 cm | ≈ 14 Hz? | ≈ 23 cm? |
| Dunig hackspett | 31 cm | 14 Hz | 29 cm |
| European Starling | 35 cm | 14 Hz | 26 cm |
Genom att medelvärdet av alla 6 värdena kan vi uppskatta att en genomsnittlig europeisk svalor flyger med marschfart med en frekvens på ungefär 15 slag per sekund och en amplitud på ungefär 22 cm.
Hoppa lite, broder
Förra månadens artikel om The Strouhal Number in Cruising Flight visade hur förenklade flygvågformer som graf amplitud kontra våglängd kan vara användbar för att visualisera Strouhal-förhållandet (fA / U), en måttlös parameter som tenderar att falla i intervallet 0,2–0,4 under effektiv kryssningsflygning.
För en europeisk sval som flyger med vår uppskattade vingbeatsamplitud på 24 cm varierar det förutspådda mönstret för kryssningsflyg från ett Strouhal-nummer ( St) av 0,2:
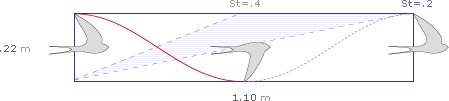
… till en mindre effektiv 0,4:
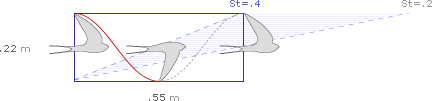
Om det första diagrammet (St = 0,2) är korrekt, skulle marschhastigheten för European Swallow vara ungefär 16 meter per sekund (15 slag per sekund * 1,1 meter per takt). Om det andra diagrammet (St = 0,4) är korrekt, skulle marschhastigheten för den europeiska svalan vara närmare 8 meter per sekund (15 slag per sekund * 0,55 meter per takt).
Om vi löser oss på ett mellanliggande Strouhal-värde på 0,3:
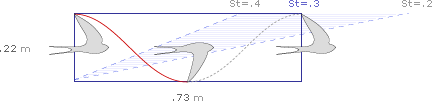
Vi kan uppskatta den europeiska svalans hastighet till ungefär 11 meter per sekund (15 slag per sekund * 0,73 meter per takt).
Tre ska vara det antal du ska räkna
Flyghastighet kan också förutsägas med en publicerad formel. Genom att invertera detta mittpunkt Strouhal-förhållande på 0,3 (fA / U ≈ 0,3), Graham K. Taylor et al. visa att som en tumregel är ett flygande djurs hastighet ungefär 3 gånger frekvens gånger amplitud (U ≈ 3fA) .5
Vi behöver nu bara ansluta siffrorna:
U ≈ 3fA
f ≈ 15 (slag per sekund)
A ≈ 0,22 (meter per takt)
U ≈ 3 * 15 * 0,22 ≈ 9,9
… för att uppskatta att lufthastighetshastigheten för en oladdad europeisk svalja är 10 meter per sekund.
Åh, ja, jag håller med om det
Med en del ytterligare studier blev det klart att dessa uppskattningar är korrekta, men kanske en tillfällighet.
En faktisk studie av två europeiska svalor som flyger i en lågturbulent vindtunnel i Lund, Sverige, visar att svalor slår sina vingar mycket långsammare än min uppskattning, med bara 7–9 slag per sekund:
”Jämfört med andra arter av liknande storlek har svalan ganska låg vingslagfrekvens och relativt långa vingar.” 7
Den maximala hastigheten fåglarna kunde upprätthålla var 13–14 meter per sekund, och även om Lundstudien inte särskilt diskuterar kryssningsflyg, är den mest effektiva flaxningen (7 slag per sekund) inträffade vid en lufthastighet i intervallet 8–11 meter per sekund, med en amplitud på 90–100 & deg (17–19 cm).
Och det var mycket glädje
Genomsnitt av ovanstående siffror och anslutning till Strouhal-ekvationen för kryssningsflyg (fA / U = 7 slag per sekund * 0,18 meter per slag / 9,5 meter per sekund) ger ett Strouhal-tal på ungefär 0,13:

… vilket indikerar ett överraskande effektivt flygmönster som faller långt under det förväntade intervallet 0,2–0,4.
Även om ett definitivt svar naturligtvis skulle kräva ytterligare mätningar, publicerade artövergripande medelvärden av vinglängd och kroppsmassa, initiala Strouhal-uppskattningar baserade på dessa medelvärden och jämförelser mellan arter, Lundvinden onödig studie av fåglar som flyger med olika hastigheter och reviderade Strouhal-siffror baserat på den studien leder mig alla till att uppskatta att den genomsnittliga krysshastigheten för en olastad europeisk svalja är ungefär 11 meter per sekund, eller 24 miles i timmen.
Vad är huvudstaden i Assyrien?
För de som letar efter ytterligare svar var de fyra huvudstäderna i Assyrien Ashur (eller Qalat Sherqat), Calah (eller Nimrud), den kortlivade Dur Sharrukin (eller Khorsabad) och Nineve.8 Ruinerna av alla fyra forntida städer faller inom det moderna staten Irak.
Tack till alla som har skrivit in med kommentarer och frågor. Svar publiceras här tillsammans med en reviderad uppskattning från Dr Graham Taylor och några alternativa teorier.
- Chris & Tilde Stuart
Birds of Africa: From Seabirds till fröätare
MIT Press (1999) - G. L. Maclean – Roberts ’Birds of Southern Africa – John Voelcker Bird Book Fund, Kapstaden, Sydafrika (1985)
- Graham Chapman, John Cleese, Eric Idle, Terry Gilliam, Terry Jones , Michael Palin
Monty Python and the Holy Grail
Python (Monty) Pictures Ltd. (1975) - Avian Demography Unit
SAFRING resultat av den europeiska svalan (Hirundo rustica)
Institutionen för statistikvetenskaper, University of Cape Town (2002) - Graham K. Taylor, Robert L. Nudds, Adrian LR Thomas
Kryssning med flygande och simmande djur på ett Strouhal-nummer inställd för hög effektivitet
Nature 425, 707–711 (16 oktober 2003) - E-postkorrespondens med Graham Taylor från University of Oxford Zoology Department (22–23 oktober 2003)
- Kirsty J. Park, Mikael Rosén, Anders Hedenström
Flygkematematik av ladugården (Hirundo rustica) över ett stort antal hastigheter i en vindtunnel
Journal of Experimental Biology 204, 2741–2750 (2001) - Ashur Cherry
Assyrisk historia – Mesopotamian Encyclopedia (2001)