Lernziele
- Geben Sie die De-Broglie-Wellengleichung an.
- Verwendung Diese Gleichung zur Berechnung der Wellenlänge eines sich bewegenden Objekts.
Jenseits von Bohrs Modell
Bohrs Modell des Atoms war wertvoll, um zu demonstrieren, wie Elektronen waren in der Lage, Energie zu absorbieren und freizusetzen und wie Atomemissionsspektren erzeugt wurden. Das Modell erklärte jedoch nicht wirklich, warum Elektronen nur in festen Kreisbahnen existieren sollten, anstatt in einer unbegrenzten Anzahl von Bahnen mit unterschiedlichen Energien existieren zu können. Um zu erklären, warum Atomenergiezustände quantisiert werden, mussten Wissenschaftler die Art und Weise überdenken, in der sie die Natur des Elektrons und seine Bewegung betrachteten.
Plancks Untersuchung der Emissionsspektren heißer Objekte und die nachfolgenden Untersuchungen zum photoelektrischen Effekt hatten gezeigt, dass Licht sich sowohl als Welle als auch als Teilchen verhalten kann. Es schien vernünftig, sich zu fragen, ob Elektronen auch eine Doppelwellenteilchen-Natur haben könnten. Der französische Wissenschaftler Louis de Broglie (1892–1987) leitete 1924 eine Gleichung ab, die die Wellennatur eines Teilchens beschrieb. Insbesondere ist die Wellenlänge (λ) eines sich bewegenden Objekts gegeben durch:
\ displaystyle \ lambda = \ frac {h} {mv}
In dieser Gleichung ist h die Plancksche Konstante , m ist die Masse des Partikels in kg und v ist die Geschwindigkeit des Partikels in m / s. Das folgende Problem zeigt, wie die Wellenlänge des Elektrons berechnet wird.
Wenn wir die Wellenlänge eines 0,145 kg schweren Baseballs berechnen würden, der mit einer Geschwindigkeit von 40 m / s geworfen wird, würden wir einen extrem kurzen Wert finden Wellenlänge in der Größenordnung von 10–34 m. Diese Wellenlänge ist selbst mit fortschrittlichen wissenschaftlichen Geräten nicht zu erfassen. Während sich alle Objekte mit wellenförmiger Bewegung bewegen, bemerken wir dies nie, da die Wellenlängen viel zu kurz sind. Andererseits sind Partikel mit messbaren Wellenlängen alle sehr klein. Die Wellennatur des Elektrons erwies sich jedoch als Schlüsselentwicklung für ein neues Verständnis der Natur des Elektrons. Ein Elektron, das auf einen bestimmten Raum um den Kern eines Atoms beschränkt ist, kann sich nur so um dieses Atom bewegen, dass seine Elektronenwelle der Größe des Atoms korrekt „entspricht“. Dies bedeutet, dass die Frequenzen von Elektronenwellen quantisiert werden. Basierend auf der E = hv-Gleichung bedeuten die quantisierten Frequenzen, dass Elektronen in einem Atom nur bei bestimmten Energien existieren können, wie Bohr zuvor theoretisiert hatte.
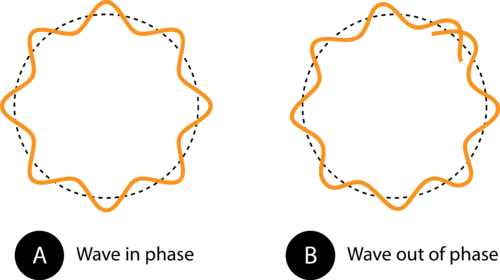
Abbildung 1. Der Umfang der Umlaufbahn in (A) ermöglicht es der Elektronenwelle, perfekt in die Umlaufbahn zu passen. Dies ist eine zulässige Umlaufbahn. In (B) tut dies die Elektronenwelle nicht passen richtig in die Umlaufbahn, daher ist diese Umlaufbahn nicht zulässig.
Zusammenfassung
- Die deBroglie-Wellengleichungen ermöglichen die Berechnung der Wellenlänge jeder Bewegung Objekt.
- Wenn die Geschwindigkeit des Elektrons abnimmt, nimmt seine Wellenlänge zu.
Übung
Verwenden Sie den Link unten, um Berechnungen mit zu üben die deBroglie-Wellengleichung:
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
Überprüfen Sie
- Was Hat das Bohr-Modell nicht erklärt?
- Geben Sie die DeBroglie-Wellengleichung an.
- Was passiert, wenn die Geschwindigkeit des Elektrons abnimmt?