Learning Cíle
- Uveďte de Broglieovu vlnovou rovnici.
- Použití tato rovnice pro výpočet vlnové délky pohybujícího se objektu.
Beyond Bohr’s Model
Bohrův model atomu byl cenný pro demonstraci toho, jak elektrony byli schopni absorbovat a uvolňovat energii a jak byla vytvořena atomová emisní spektra. Model však ve skutečnosti nevysvětlil, proč by elektrony měly existovat pouze na pevných kruhových drahách, než aby mohly existovat v neomezeném počtu drah všech s různými energiemi. Abychom vysvětlili, proč jsou stavy atomové energie kvantizovány, vědci potřebovali přehodnotit způsob, jakým pohlíželi na povahu elektronu a jeho pohyb.
Planckovo zkoumání emisních spekter horkých objektů a následné studie fotoelektrického jevu prokázaly, že světlo je schopné chovat se jako vlna i jako částice. Připadalo mi rozumné uvažovat o tom, zda by elektrony mohly mít také povahu dvouvlnných částic. V roce 1924 francouzský vědec Louis de Broglie (1892–1987) odvodil rovnici popisující vlnovou povahu jakékoli částice. Vlnová délka (λ) libovolného pohybujícího se objektu je dána vztahem:
\ displaystyle \ lambda = \ frac {h} {mv}
V této rovnici je h Planckova konstanta , m je hmotnost částice v kg a v je rychlost částice v m / s. Níže uvedený problém ukazuje, jak vypočítat vlnovou délku elektronu.
Pokud bychom měli vypočítat vlnovou délku 0,145 kg baseballu vrhaného rychlostí 40 m / s, přišli bychom s extrémně krátkou vlnová délka řádově 10–34 m. Tuto vlnovou délku nelze detekovat ani s pokročilým vědeckým vybavením. Zatímco se všechny objekty pohybují vlnovým pohybem, nikdy si toho nevšimneme, protože vlnové délky jsou příliš krátké. Na druhou stranu jsou částice s měřitelnými vlnovými délkami velmi malé. Vlnová povaha elektronu se však ukázala jako klíčový vývoj v novém chápání podstaty elektronu. Elektron, který je omezen na určitý prostor kolem jádra atomu, se může pohybovat kolem tohoto atomu pouze takovým způsobem, že jeho elektronová vlna „odpovídá“ velikosti atomu správně. To znamená, že frekvence elektronových vln jsou kvantovány. Kvantované frekvence na základě rovnice E = hv znamenají, že elektrony mohou existovat v atomu pouze při specifických energiích, jak dříve předpokládal Bohr.
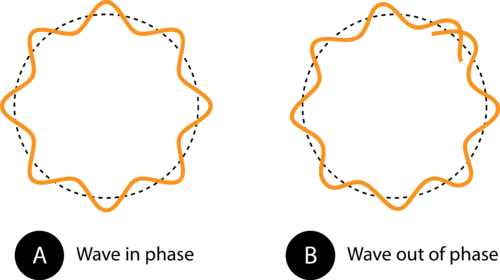
Obrázek 1. Obvod oběžné dráhy v (A) umožňuje, aby elektronová vlna dokonale zapadala do oběžné dráhy. Toto je povolená oběžná dráha. V (B) elektronová vlna správně zapadnout na oběžnou dráhu, takže tato oběžná dráha není povolena.
Souhrn
- Vlnové rovnice deBroglie umožňují výpočet vlnové délky jakéhokoli pohybujícího se objekt.
- Jak se snižuje rychlost elektronu, zvyšuje se jeho vlnová délka.
Cvičení
Použijte odkaz níže procvičovat výpočty pomocí rovnice deBroglieho vlny:
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
Recenze
- Co nevysvětlil Bohrův model?
- Uveďte deBroglieovu vlnovou rovnici.
- Co se stane, když se rychlost elektronu sníží?