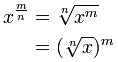Også kaldet “Radikale” eller “Rationelle eksponenter”
Eksponenter for hele antallet
Lad os først se på hele antallet eksponenter:

Eksponenten for et tal siger, hvor mange gange nummeret skal bruges i en multiplikation.
I dette eksempel: 82 = 8 × 8 = 64
Et andet eksempel: 53 = 5 × 5 × 5 = 125
Brøkeksponenter
Men hvad nu hvis eksponenten er en brøkdel?
|
En eksponent på 12 er faktisk kvadratrod En eksponent på 13 er terningsrot En eksponent på 14 er 4. rod Og så videre! |
 |
Hvorfor?
Lad os se hvorfor i en eksempel.
For det første fortæller lovene om eksponenter os, hvordan vi skal håndtere eksponenter, når vi multiplicerer:
Eksempel: x2x2 = (xx) (xx) = xxxx = x4
Hvilket viser, at x2x2 = x (2 + 2) = x4
Så lad os prøve det med fraktionerede eksponenter:
Prøv en anden brøk
Lad os prøve det igen, men med en eksponent på en fjerdedel (1/4):
Eksempel:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Så 16¼ brugt 4 gange i en multiplikation giver 16,
og så er 16¼ en 4. rod af 16
Generel regel
Det fungerede i ½, det fungerede med ¼, faktisk fungerer det generelt:
x1 / n = Den niende rod af x
Så vi kan komme med dette:
| |
|
Eksempel: Hvad er 271/3?
Svar: 271/3 = ![]() 27 = 3
27 = 3
Hvad med mere komplicerede fraktioner?
Hvad med en fraktioneret eksponent som 43/2?
Det betyder virkelig at lave en terning (3) og en kvadratrod (1/2) i enhver rækkefølge.
Lad mig forklare.
En brøk (som m / n) kan opdeles i to dele:
- en heltaldel (m) og
- en brøk (1 / n) del
Så fordi m / n = m × (1 / n) kan vi gøre dette:
Rækkefølgen betyder ikke noget, så det fungerer også for m / n = (1 / n) × m:
Og vi får dette:
| |
|
Nogle eksempler:
Eksempel : Hvad er 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
eller
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
Uanset hvad får det samme resultat.
Eksempel: Hvad er 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
eller
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
Det var bestemt lettere 2. vej!
Nu … Spil med grafen!
Se hvor glat kurven ændres, når du spiller med brøkene i denne animation, dette viser dig, at denne idé om fraktionerede eksponenter passer fint sammen:
Ting at prøve:
- Start med m = 1 og n = 1, og øg derefter langsomt n så du kan se 1/2, 1/3 og 1/4
- Prøv derefter m = 2 og skub n op og ned for at se brøker som 2/3 osv.
- Prøv nu at gøre eksponenten -1
- Endelig prøv at øge m, derefter reducere n, derefter reducere m, derefter øge n: kurven skal gå rundt og omkring