Introduktion til sæt

Definition

Hvad er et sæt? Kort sagt, det er en samling.

Først angiver vi en fælles egenskab blandt “ting” (vi definerer dette ord senere), og derefter samler vi alle de “ting”, der har denne fælles ejendom.

For eksempel de ting, du har på: hat, skjorte, jakke, bukser osv.

Jeg er sikker på, at du kunne komme med mindst hundrede.

Dette kaldes et sæt.

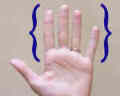
Eller et andet eksempel er fingertyper. Dette sæt inkluderer indeks, mellem, ring og pinky.

Så det er bare ting grupperet sammen med en bestemt egenskab til fælles.

Notation

Der er en ret simpel notation for sæt. Vi lister blot hvert element (eller “medlem”) adskilt af et komma og sætter derefter nogle krøllede parenteser omkring det hele:

Dette er notationen for de to foregående eksempler:

{sokker, sko, ure, skjorter, …}
{indeks, mellem, ring, lyserød}

Bemærk hvordan det første eksempel har “…” (tre prikker sammen) .

Så det betyder, at det første eksempel fortsætter … … for uendelig.

(OK, der er ikke en uendelig mængde ting, du kan bære, men det er jeg ikke helt sikker på! Efter en times tænkning af forskellige ting, jeg stadig ikke sikker. Så lad os bare sige, at det er uendeligt for dette eksempel.)

Så:

Men nogle gange kan “…” bruges i midten til at gemme skrivning af lange lister:

Numeriske sæt

Så hvad har dette med matematik at gøre? Når vi definerer et sæt, er alt, hvad vi skal specificere, en fælles egenskab. Hvem siger, at vi ikke kan gøre det med tal?

Og så videre. Vi kan komme med alle forskellige typer sæt.

Vi kan også definere et sæt efter dets egenskaber, såsom {x | x > 0}, hvilket betyder “sæt af alle x”, således at x er større end 0 “, se Set-Builder Notation for at lære mere.

Og vi kan have sæt sæt, der ikke har nogen fælles egenskab, de er bare defineret på den måde. For eksempel:

Er alle sæt, som jeg bare tilfældigt slog på mit tastatur for at producere.

Hvorfor er sæt vigtige?

Sæt er matematikkens grundlæggende egenskab. Nu som et advarselsord synes sæt i sig selv ret meningsløse. Men det er kun når vi anvender sæt i forskellige situationer, at de bliver den stærke byggesten i matematik, som de er.

Matematik kan blive utroligt kompliceret ganske hurtigt. Grafteori, abstrakt algebra, reel analyse, kompleks Analyse, lineær algebra, talteori og listen fortsætter. Men der er en ting, som alle disse deler til fælles: Sæt.

Universalt sæt

		I starten brugte vi ordet “ting” i citater. Vi kalder dette det universelle sæt. Det er et sæt, der indeholder alt. Nå, ikke ligefrem alt. Alt, hvad der er relevant for vores spørgsmål.
		I talteori er det universelle sæt alle heltal, da talteori simpelthen er undersøgelse af heltal.
		Men i Calculus (også kendt som reel analyse) er det universelle sæt næsten altid de reelle tal.
		Og i kompleks analyse gættede du det, det universelle sæt er de komplekse tal.

Noget mere notat

Nu behøver du ikke lytte til standarden , kan du bruge noget som m til at repræsentere et sæt uden at bryde nogen matematiske love (pas på, du kan få π år i matematikfængsel for at dividere med 0), men denne notation er ret flot og let at følge, så hvorfor ikke?

Også når vi siger, at et element a er i et sæt A, bruger vi symbolet til at vise det.
Og hvis noget ikke er i en sæt brug .

Lighed

To sæt er ens, hvis de har nøjagtigt samme medlemmer. Ved første øjekast virker de måske ikke ens, så vi bliver muligvis nødt til at undersøge dem nøje!

Og ligetegnet ( =) bruges til at vise lighed, så vi skriver:

A = B

Delsæt

Når vi definerer et sæt, hvis vi tager stykker af det sæt, kan vi danne det, der kaldes et delsæt.

Generelt:

Så lad os bruge denne definition i nogle eksempler.

Lad os prøve et hårdere eksempel.

Korrekte delmængder

Hvis vi ser på definitionen af delmængder og lader vores sind vandre lidt, kommer vi til en underlig konklusion.

Lad A være et sæt. Er hvert element af A i A?

Nåja, umm, ja selvfølgelig, ikke?

Så det betyder, at A er en delmængde af A. Det er en delmængde af sig selv!

Dette virker ikke meget ordentligt, gør det? Hvis vi ønsker, at vores undergrupper skal være korrekte, introducerer vi (hvad andet end) korrekte delmængder:

Dette lille stykke i slutningen er der for at sikre, at A ikke er en korrekt delmængde af sig selv: vi siger, at B skal have mindst et ekstra element.

Bemærk, at når A er en korrekt delmængde af B, er det også en delmængde af B.

Endnu mere notering

Når vi siger, at A er en delmængde af B, skriver vi A B.

Eller vi kan sige, at A ikke er en delmængde af B af A B (“A er ikke en delmængde af B”)

Når vi taler om korrekte delmængder, vi tager linjen nedenunder ud, så det bliver A B, eller hvis vi vil sige det modsatte, A B.

Tom (eller nul) sæt

Dette er sandsynligvis den mærkeligste ting ved sæt.

Tænk som eksempel på sæt klavernøgler på en guitar.

“Men vent!” du siger, “Der er ingen klavernøgler på en guitar! “

Og det har du ret. Det er et sæt uden elementer.

Dette er kendt som det tomme sæt (eller Null Set). Der er ikke nogen elementer i det. Ikke et. Nul.

Det er repræsenteret af

Eller af {} (et sæt uden elementer)

Nogle andre eksempler på det tomme sæt er sættet af lande syd for sydpolen.

Så hvad er der så underligt ved det tomme sæt? Den del kommer dernæst.

Tomt sæt og undersæt

Så lad os vende tilbage til vores definition af delmængder. Vi har et sæt A. Vi definerer det ikke noget mere end det kunne det være ethvert sæt. Er det tomme sæt et undersæt af A?

Går vi tilbage til vores definition af undergrupper, hvis hvert element i det tomme sæt også er i A, så er det tomme sæt et undersæt af A. Men hvad hvis vi har ingen elementer?

Det kræver en introduktion til logikken for at forstå dette, men denne udsagn er en, der er “vakuum” eller “trivielt” sand.

En god måde at tænke på det er: vi kan ikke finde nogen elementer i det tomme sæt, der ikke er i A, så det må være, at alle elementer i det tomme sæt er i A.

Så svaret på det stillede spørgsmål er et rungende ja.

Bestilling

Nej, ikke rækkefølgen af elementerne. I sæt betyder det ikke noget i hvilken rækkefølge elementerne er.

Et endeligt sæt har en endelig rækkefølge (eller kardinalitet). Et uendeligt sæt har uendelig rækkefølge (eller kardinalitet).

For endelige sæt er rækkefølgen (eller kardinaliteten) antallet af elementer.

For uendelige sæt kan vi kun sige, at rækkefølgen er uendelig. Mærkeligt nok kan vi med sæt sige, at nogle uendelighed er større end andre, men dette er et mere avanceret emne i sæt.

Arg! Ikke mere notation!

Nej, bare en sjov. Ikke mere notation.

af

og