Hvad er standardafvigelse? | STDEV.P | STDEV.S | Varians
Denne side forklarer, hvordan man beregner standardafvigelsen baseret på hele populationen ved hjælp af STDEV.P-funktionen i Excel, og hvordan man estimerer standardafvigelsen baseret på en prøve ved hjælp af STDEV.S-funktionen i Excel.
Hvad er standardafvigelse?
Standardafvigelse er et tal, der fortæller dig, hvor langt tal er fra deres gennemsnit.
1. For eksempel har nedenstående tal et gennemsnit (gennemsnit) på 10.
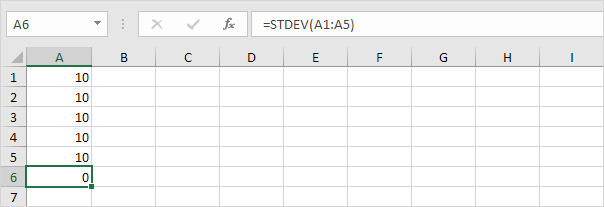
Forklaring: tallene er alle de samme, som betyder, at der ikke er nogen variation. Som et resultat har tallene en standardafvigelse på nul. STDEV-funktionen er en gammel funktion. Microsoft Excel anbefaler, at du bruger den nye STEDV.S-funktion, der giver nøjagtigt det samme resultat.
2. Nedenstående tal har også et gennemsnit (gennemsnit) på 10.
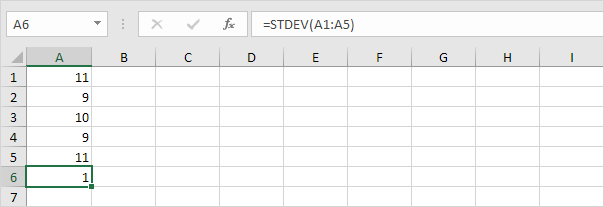
Forklaring: tallene er tæt på gennemsnittet. Som et resultat har tallene en lav standardafvigelse.
3. Tallene nedenfor har også et gennemsnit (gennemsnit) på 10.
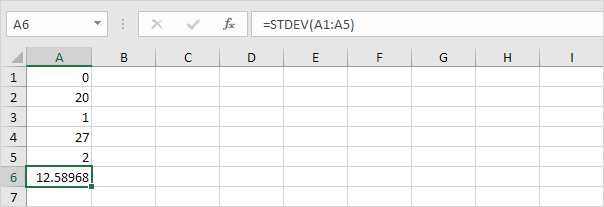
Forklaring: tallene er spredt. Som et resultat har tallene en høj standardafvigelse.
STDEV.P
STDEV.P-funktionen (P står for Population) i Excel beregner standardafvigelsen baseret på hele befolkningen. For eksempel underviser du i en gruppe på 5 studerende. Du har testresultaterne for alle studerende. Hele befolkningen består af 5 datapunkter. STDEV.P-funktionen bruger følgende formel:
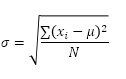
I dette eksempel er x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (gennemsnit), N = 5 (antal datapunkter).
1. Beregn gennemsnittet (μ).
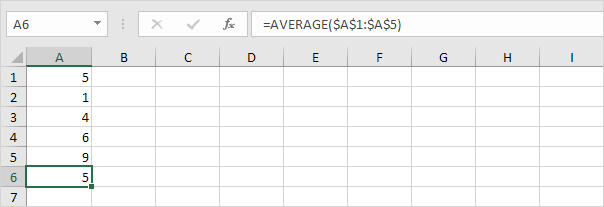
2. For hvert nummer beregnes afstanden til gennemsnittet.
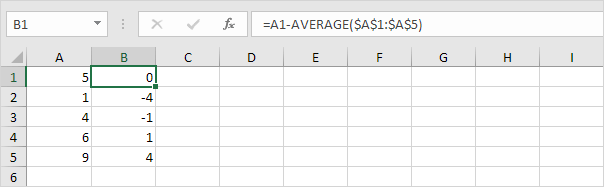
3. Kvadrerer denne afstand for hvert nummer.
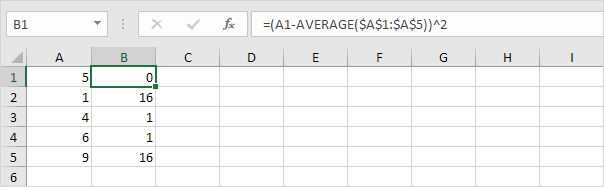
4. Summen (∑) af disse værdier.
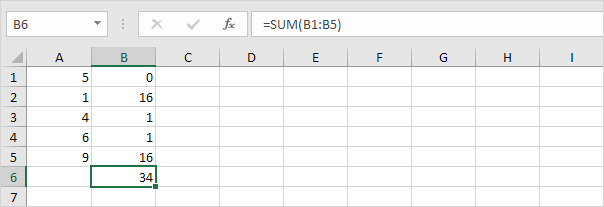
5. Opdel med antallet af datapunkter (N = 5).
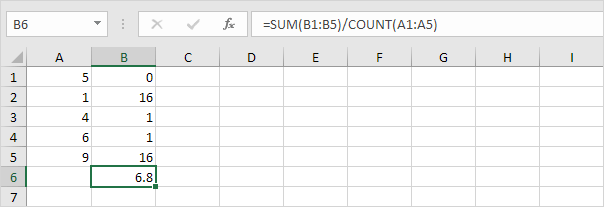
6. Tag kvadratroden.
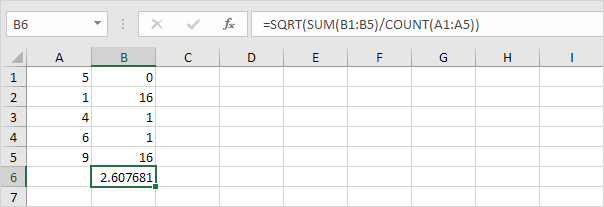
7. Heldigvis kan STDEV.P-funktionen i Excel udføre alle disse trin for dig.
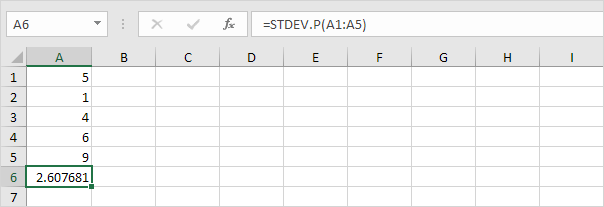
STDEV.S
STDEV.S-funktionen (S står for prøve) i Excel estimerer standardafvigelsen baseret på en prøve. For eksempel underviser du i en stor gruppe studerende. Du har kun testresultaterne på 5 studerende. Prøvestørrelsen er lig med 5. STDEV.S-funktionen bruger følgende formel:
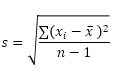
I dette eksempel er x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (samme tal som ovenfor), x̄ = 5 (prøve middelværdi), n = 5 (prøvestørrelse).
1. Gentag trin 1-5 ovenfor, men ved trin 5 divideres med n-1 i stedet for N.
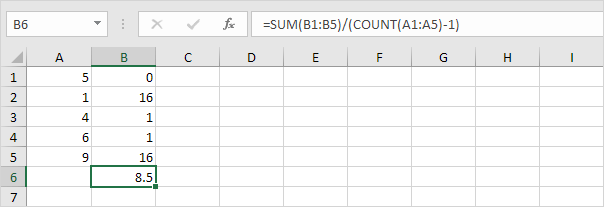
2. Tag kvadratroden.
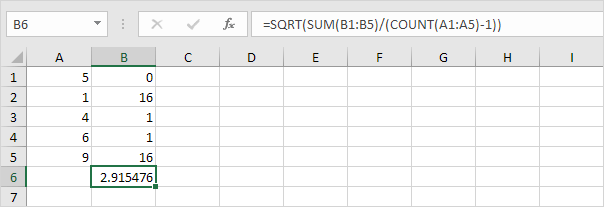
3. Heldigvis kan STDEV.S-funktionen i Excel udføre alle disse trin for dig.
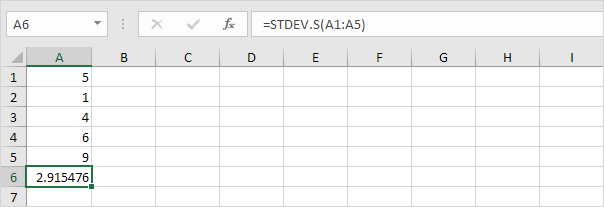
Bemærk: hvorfor deler vi efter n – 1 i stedet for ved n når vi estimerer standardafvigelsen baseret på en prøve? Bessels korrektion angiver, at dividering med n-1 i stedet for med n giver et bedre estimat af standardafvigelsen.
Variance
Variant er kvadratet for standardafvigelsen. Det er så simpelt. Nogle gange er det lettere at bruge variansen til løsning af statistiske problemer.
1. VAR.P-funktionen nedenfor beregner variansen baseret på hele befolkningen.
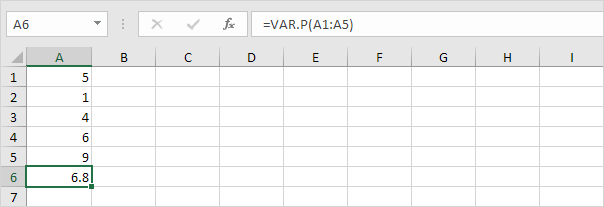
Bemærk: du kendte allerede dette svar (se trin 5 under STDEV.P). Tag kvadratroden af dette resultat for at finde standardafvigelsen baseret på hele populationen.
2. VAR.S-funktionen nedenfor estimerer variansen baseret på en prøve.
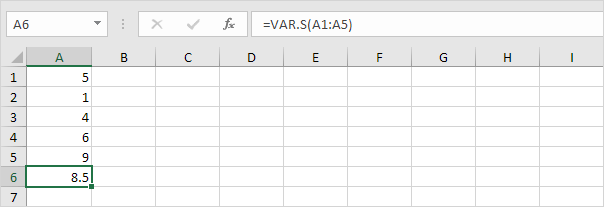
Bemærk: du kendte allerede dette svar (se trin 1 under STDEV.S). Tag kvadratroden af dette resultat for at finde standardafvigelsen baseret på en prøve.
3. VAR og VAR.S producerer nøjagtigt det samme resultat.
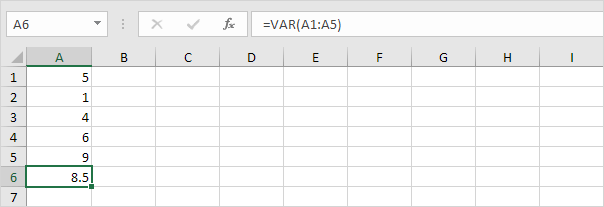
Bemærk: Microsoft Excel anbefaler, at du bruger den nye VAR.S-funktion.