Poincaré-formodningen og 6 andre komplekse matematiske teorier er blevet kaldt Millenniumprisproblemerne af Clay Mathematics Institute (CMI). Hvert problem er blevet beskrevet som et “vigtigt klassisk spørgsmål, der har modstået løsninger gennem årene”, med den første person, der udtænker en løsning, der hver tjener $ 1.000.000 med tilladelse til CMI. Som du så ovenfor, er det ikke let at løse disse problemer. feat. Et af problemerne er forblevet uløst, siden det blev formuleret i 1859 af den tyske matematiker Bernhard Riemann.
Riemann-hypotesen, opkaldt efter den førnævnte tyske matematiker, anses bredt for at være det vigtigste uløste problem i ren matematik. Det er af stor interesse for talteori, fordi det indebærer resultater om fordelingen af primtal, som bruges i alt fra biologi til kryptering og kvantemekanik. For at forstå Riemann-hypotesen skal vi først forklare et par nøgler begreber:
- Et komplekst tal er af formen a + bi, hvor i er defineret af i² = -1. I denne form er den reelle del af et komplekst tal a, og det imaginære del er bi.
- Riemann zeta-funktionen er en funktion af en kompleks variabel (en funktion af komplekse tal) defineret af følgende ligning, hvor s er ethvert andet komplekst tal end 1, og hvis værdier også er komplekse:
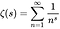
- En “nul” i en funktion er en x sådan at f (x) = 0
- De “trivielle nuller” i Riemann zeta-funktionen er alle negative lige heltal (-2, -4, -6,…)
- De “ikke-trivielle nuller ”Af Riemann zeta-funktionen er alle de andre værdier for s, for hvilke ζ (s) = 0 (dvs. s er ikke et negativt ens heltal).
Nu hvor vi har nogle definitioner nede på pat, kan vi gå videre og angive Riemann-hypotesen:
Den reelle del af ethvert ikke-trivielt nul i Riemann zeta-funktionen er 1/2
Denne (for mig i det mindste) er meget lettere at forstå end Poincaré-formodningen og virker ikke intuitivt meget vanskelig. Men det ser heller ikke ud til at betyde meget. Virkelig, hvem bekymrer sig om, hvornår denne tilfældige funktion har en værdi på 0. Det er ikke overraskende, at mange matematikere gør det, og af en meget god grund.
Nogle tal har den specielle egenskab, at de ikke kan udtrykkes. som produktet af to mindre tal (produkt er multiplikation), dvs. 2,3,5,7,11 osv. Kendt som primtal, de er på en måde de enkleste tal, du kan få, og danner byggestenene til alle andre tal. Frustrerende synes primtal imidlertid ikke at følge noget mønster. 3137 er et primtal, og det næste derefter er først i 3163, men derefter følger 3167 og 3169 hurtigt efter hinanden, som alle er primtal. I en nøddeskal, hvis du finder et primtal, er der ingen måde at fortælle, hvor den næste vil være uden at kontrollere alle tallene, mens du går. Ved hjælp af Prime Number Theorem (PNT) kan du finde ud af, hvor mange primtal der er under en bestemt tærskel.
Prime Number Theorem er kun et skøn med forskellige værdier, der giver en anden sandsynlighed for at være korrekt, men aldrig 100% sikkerhed. Forstå dog antagelsen om, at Reimann-hypotesen er sand, du kan oprette en matematisk tilnærmelse, der kombinerer primtaltalteoremet og de ikke-trivielle nuller i Riemann zeta-funktionen for at fejlkorrigere de interne komponenter, hvilket giver den “bedst mulige” grænse for fejludtrykket i primtaltalssætningen. Hvis det var muligt at bevise Reimann-hypotesen fuldstændigt, ville dette give PNT muligheden for at give utroligt tætte estimater til den faktiske værdi og åbne mange muligheder inden for forskellige grene af matematik. der er mange vigtige hypoteser, at det at være med “Hvis Riemann-hypotesen er sand, så …”, så at løse dette problem også med det samme ville validere alle de efterfølgende antagelser.