¿Qué es la desviación estándar? | STDEV.P | STDEV.S | Varianza
Esta página explica cómo calcular la desviación estándar basada en toda la población usando la función STDEV.P en Excel y cómo estimar la desviación estándar basada en una muestra usando la función STDEV.S en Excel.
¿Qué es la desviación estándar?
La desviación estándar es un número que le indica qué tan lejos están los números de su media.
1. Por ejemplo, los números siguientes tienen una media (promedio) de 10.
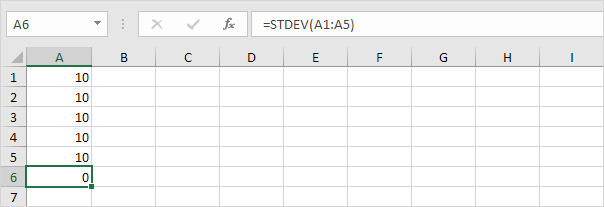
Explicación: los números son todos iguales que significa que no hay variación. Como resultado, los números tienen una desviación estándar de cero. La función STDEV es una función antigua. Microsoft Excel recomienda usar la nueva función STEDV.S que produce exactamente el mismo resultado.
2. Los números siguientes también tienen una media (promedio) de 10.
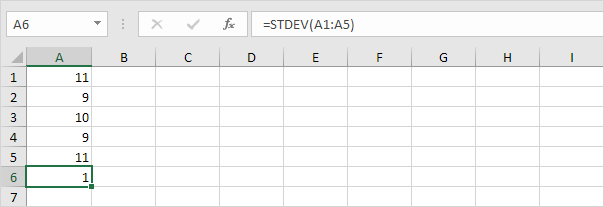
Explicación: los números están cerca de la media. Como resultado, los números tienen una desviación estándar baja.
3. Los números siguientes también tienen una media (promedio) de 10.
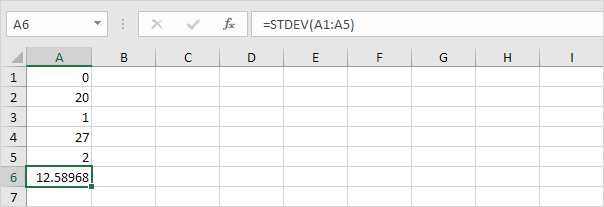
Explicación: los números están distribuidos. Como resultado, los números tienen una desviación estándar alta.
STDEV.P
La función STDEV.P (la P significa Población) en Excel calcula la desviación estándar basada en toda la población. Por ejemplo, estás enseñando a un grupo de 5 estudiantes. Tienes los puntajes de las pruebas de todos los estudiantes. Toda la población consta de 5 puntos de datos. La función DESVEST.P utiliza la siguiente fórmula:
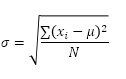
En este ejemplo, x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (media), N = 5 (número de puntos de datos).
1. Calcule la media (μ).
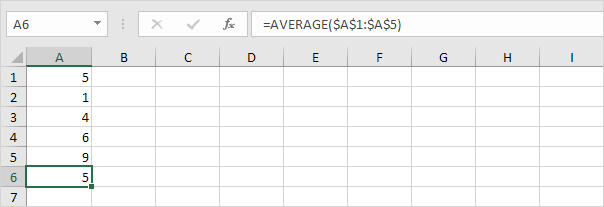
2. Para cada número, calcule la distancia a la media.
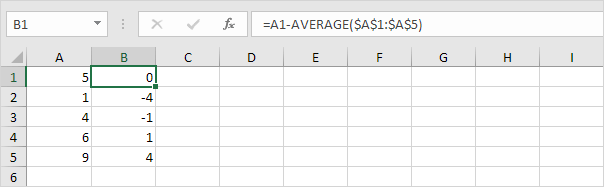
3. Para cada número, eleva al cuadrado esta distancia.
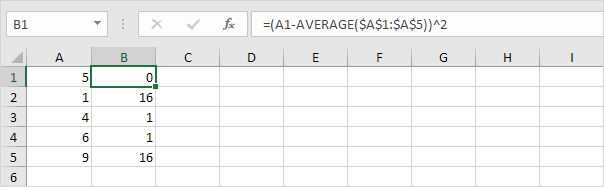
4. Suma (∑) estos valores.
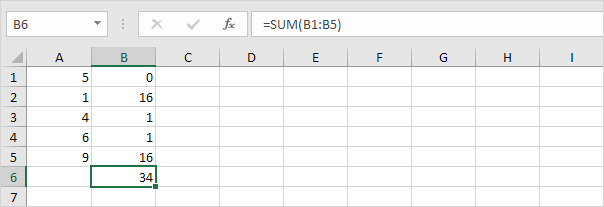
5. Dividir por la cantidad de puntos de datos (N = 5).
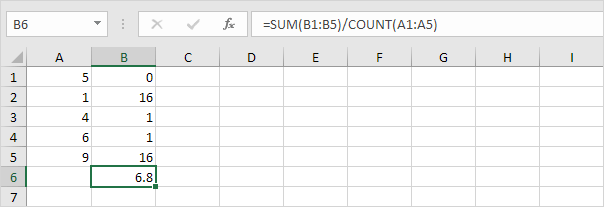
6. Saca la raíz cuadrada.
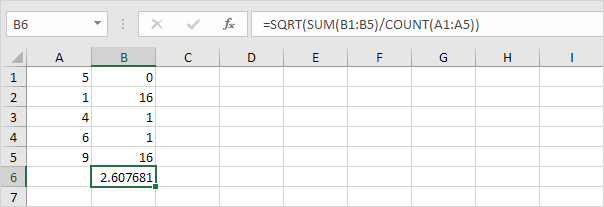
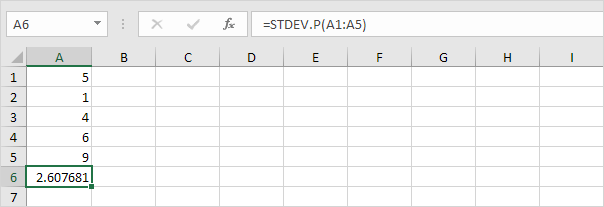
7. Afortunadamente, la función STDEV.P en Excel puede ejecutar todos estos pasos por usted.
STDEV.S
La función DESVEST.S (la S significa Muestra) en Excel estima la desviación estándar basada en una muestra. Por ejemplo, está enseñando a un grupo grande de estudiantes. Solo tiene los puntajes de las pruebas de 5 estudiantes. El tamaño de la muestra es igual a 5. La función DESVEST.S utiliza la siguiente fórmula:
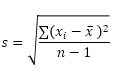
En este ejemplo, x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (los mismos números que arriba), x̄ = 5 (ejemplo media), n = 5 (tamaño de muestra).
1. Repita los pasos 1 a 5 anteriores, pero en el paso 5 divida por n-1 en lugar de N.
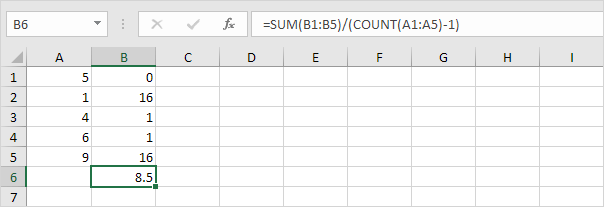
2. Saca la raíz cuadrada.
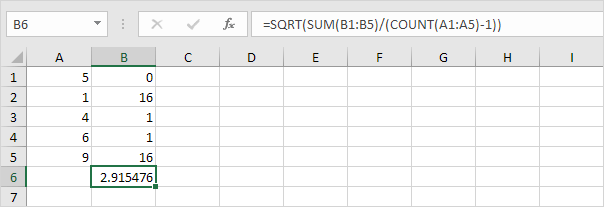
3. Afortunadamente, la función STDEV.S en Excel puede ejecutar todos estos pasos por usted.
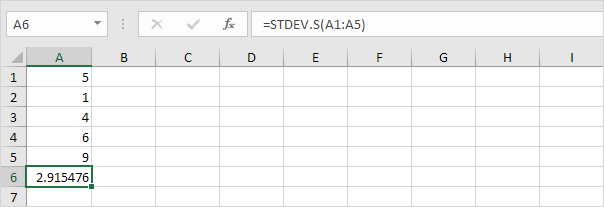
Nota: ¿por qué dividimos por n – 1 en lugar de n cuando estimamos la desviación estándar en función de una muestra? La corrección de Bessel establece que dividir por n-1 en lugar de por n da una mejor estimación de la desviación estándar.
Varianza
La varianza es el cuadrado de la desviación estándar. Es así de simple. A veces es más fácil usar la varianza al resolver problemas estadísticos.
1. La función VAR.P a continuación calcula la varianza basándose en la población completa.
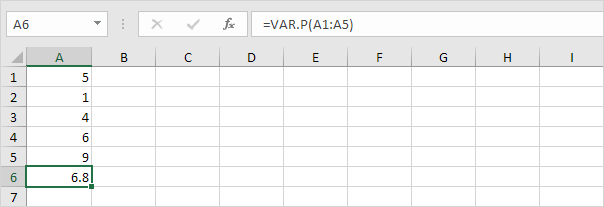
Nota: ya conocía esta respuesta (consulte paso 5 en STDEV.P). Obtenga la raíz cuadrada de este resultado para encontrar la desviación estándar basada en toda la población.
2. La función VAR.S a continuación estima la varianza según una muestra.
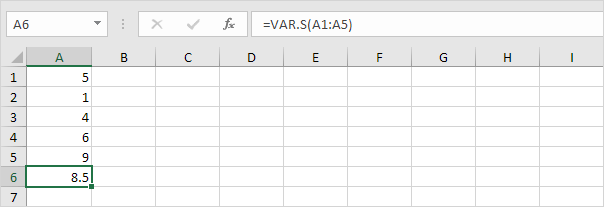
Nota: ya conocía esta respuesta (consulte el paso 1 en STDEV.S). Saca la raíz cuadrada de este resultado para encontrar la desviación estándar basada en una muestra.
3. VAR y VAR.S producen exactamente el mismo resultado.
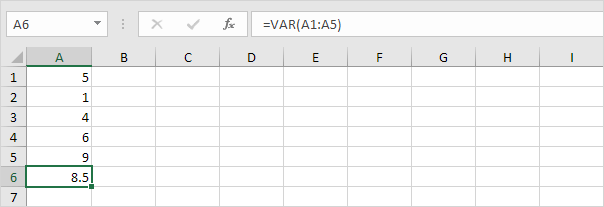
Nota: Microsoft Excel recomienda utilizar la nueva función VAR.S.