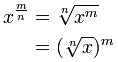También llamados «radicales» o «exponentes racionales»
Exponentes de números enteros
Primero, veamos los números enteros exponentes:

El exponente de un número dice cuántas veces se debe usar el número en una multiplicación.
En este ejemplo: 82 = 8 × 8 = 64
Otro ejemplo: 53 = 5 × 5 × 5 = 125
Exponentes fraccionarios
Pero, ¿y si el exponente es una fracción?
|
Un exponente de 12 es en realidad raíz cuadrada Un exponente de 13 es raíz cúbica Un exponente de 14 es la cuarta raíz ¡Y así sucesivamente! |
 |
¿Por qué?
Veamos por qué en un ejemplo.
Primero, las leyes de los exponentes nos dicen cómo manejar exponentes cuando multiplicamos:
Ejemplo: x2x2 = (xx) (xx) = xxxx = x4
Lo que muestra que x2x2 = x (2 + 2) = x4
Intentemos eso con exponentes fraccionarios:
Prueba con otra fracción
Intentemos eso de nuevo, pero con un exponente de un cuarto (1/4):
Ejemplo:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Entonces 16¼ usado 4 veces en una multiplicación da 16,
y entonces 16¼ es un 4ta raíz de 16
Regla general
Funcionó para ½, funcionó con ¼, de hecho funciona en general:
x1 / n = La raíz n-ésima de x
Entonces podemos pensar en esto:
| |
|
Ejemplo: ¿Qué es 271/3?
Respuesta: 271/3 = ![]() 27 = 3
27 = 3
¿Qué pasa con las fracciones más complicadas?
¿Qué pasa con un exponente fraccionario como 43/2?
Eso es realmente decir hacer un cubo (3) y una raíz cuadrada (1/2), en cualquier orden.
Déjame explicarte.
Una fracción (como m / n) se puede dividir en dos partes:
- una parte de número entero (m) y
- una fracción (1 / n) parte
Entonces, debido a que m / n = m × (1 / n) podemos hacer esto:
El orden no importa, entonces también funciona para m / n = (1 / n) × m:
Y obtenemos esto:
| |
|
Algunos ejemplos:
Ejemplo : ¿Qué es 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
o
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
De cualquier manera se obtiene el mismo resultado.
Ejemplo: ¿Qué es 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
o
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
¡Ciertamente fue más fácil la segunda forma!
Ahora … ¡Juegue con el gráfico!
Vea lo suavemente que cambia la curva cuando juega con las fracciones en esta animación, esto le muestra que esta idea de exponentes fraccionarios encaja muy bien:
Cosas para probar:
- Comience con m = 1 y n = 1, luego aumente lentamente n para que pueda ver 1/2, 1/3 y 1/4
- Luego, intente m = 2 y deslice n hacia arriba y hacia abajo para ver fracciones como 2/3, etc.
- Ahora intente hacer el exponente -1
- Por último, intente aumentar m, luego reducir n, luego reducir m, luego aumentar n: la curva debe dar vueltas y vueltas