La Conjetura de Poincaré y otras 6 teorías matemáticas complejas han sido denominadas Problemas del Premio del Milenio por el Clay Mathematics Institute (CMI). Cada problema ha sido descrito como una «cuestión clásica importante que ha resistido soluciones a lo largo de los años», y la primera persona en idear una solución para cada uno gana $ 1,000,000 por cortesía de CMI. Sin embargo, como vio anteriormente, resolver estos problemas no es fácil Uno de los problemas ha permanecido sin resolver desde su formulación en 1859 por el matemático alemán Bernhard Riemann.
La Hipótesis de Riemann, que lleva el nombre del matemático alemán antes mencionado, es ampliamente considerada como el problema sin resolver más importante en matemáticas. Es de gran interés en la teoría de números porque implica resultados sobre la distribución de números primos, que se utilizan en todo, desde la biología hasta el cifrado y la mecánica cuántica. Para comprender la hipótesis de Riemann, primero debemos explicar algunas claves conceptos:
- Un número complejo es de la forma a + bi, donde i se define por i² = -1. De esta forma, la parte real de un número complejo es a, y el imaginario la parte es bi.
- La función zeta de Riemann es una función de una variable compleja (una función de números complejos) definida por la siguiente ecuación, donde s es cualquier número complejo que no sea 1, y cuyos valores también son complejos:
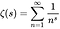
- Un «cero» de una función es una x tal que f (x) = 0
- Los «ceros triviales» de la función zeta de Riemann son todos los enteros pares negativos (-2, -4, -6,…)
- Los «ceros no triviales ”De la función zeta de Riemann son todos los demás valores de s para los cuales ζ (s) = 0 (es decir. s no es un número entero par negativo).
Ahora que tenemos algunas definiciones, podemos seguir adelante y establecer la Hipótesis de Riemann:
La parte real de cada cero no trivial de la función zeta de Riemann es 1/2
Este (para mí al menos) es mucho más fácil de entender que la Conjetura de Poincaré y no parece intuitivamente muy difícil. Sin embargo, tampoco parece significar mucho. Realmente, ¿a quién le importa cuándo esta función aleatoria tiene un valor de 0? Bueno, no es sorprendente que muchos matemáticos lo tengan, y por una muy buena razón.
Algunos números tienen la propiedad especial de que no se pueden expresar como el producto de dos números más pequeños (el producto es la multiplicación), es decir. 2, 3, 5, 7, 11, etc. Conocidos como números primos, en cierto sentido son los números más simples que se pueden obtener y forman los bloques de construcción de todos los demás números. Sin embargo, resulta frustrante que los números primos no sigan ningún patrón. 3137 es un número primo, y el siguiente no es hasta 3163, pero luego 3167 y 3169 siguen en rápida sucesión, todos los cuales son primos. En pocas palabras, si encuentra un número primo, no hay forma de saber dónde estará el siguiente sin verificar todos los números sobre la marcha. Sin embargo, usando el Teorema de los números primos (PNT), puede encontrar cuántos números primos hay por debajo de un cierto umbral.
El Teorema de los números primos es solo una estimación, con diferentes valores que dan una probabilidad diferente de ser correcto, pero nunca 100% seguro. Sin embargo, comprenda la suposición de que la hipótesis de Reimann es verdadera, puede crear una aproximación matemática combinando el Teorema del número primo y los ceros no triviales de la función zeta de Riemann para corregir el error de los componentes internos, proporcionando el «mejor posible» límite para el término de error en el Teorema de los números primos. Si fuera posible probar la Hipótesis de Reimann completamente, esto le daría al PNT la capacidad de proporcionar estimaciones increíblemente cercanas al valor real, abriendo muchas posibilidades en diferentes ramas de las matemáticas. Hay muchas hipótesis importantes de que estar con «Si la hipótesis de Riemann es cierta, entonces …», por lo que resolver este problema validaría instantáneamente todas las conjeturas posteriores también.