Olvídese de todo lo que sabe sobre números.
De hecho, olvídese de que sabe qué es un número.
Este es donde comienzan las matemáticas.
En lugar de matemáticas con números, ahora pensaremos en matemáticas con «cosas».
Definición
¿Qué es ¿un conjunto? Bueno, en pocas palabras, es una colección.
Primero especificamos una propiedad común entre «cosas» (definiremos esta palabra más adelante) y luego reunimos todas las «cosas» que tienen esta propiedad común.

Por ejemplo, los artículos que usa: sombrero, camisa, chaqueta, pantalones , y así sucesivamente.
Estoy seguro de que podría obtener al menos cien.
Esto se conoce como conjunto.
|
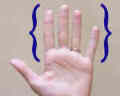
O otro ejemplo son los tipos de dedos. Este conjunto incluye índice, medio, anillo y meñique. |
 |
Por lo tanto, son solo cosas agrupadas con una determinada propiedad en común.
Notación
Hay una notación bastante simple para conjuntos. Simplemente enumeramos cada elemento (o «miembro») separado por una coma, y luego ponemos algunos corchetes alrededor de todo:

Las llaves {} a veces se denominan «llaves» o «llaves».
Esta es la notación de los dos ejemplos anteriores:
{calcetines, zapatos, relojes, camisas, …}
{índice, medio, anillo, meñique}
Observe cómo el primer ejemplo tiene el «…» (tres puntos juntos) .
Los tres puntos … se llaman puntos suspensivos y significan «continuar».
Entonces eso significa que el primer ejemplo continúa .. . para el infinito.
(Está bien, no hay realmente una cantidad infinita de cosas que puedas usar, ¡pero no estoy del todo seguro de eso! Después de una hora de pensar en cosas diferentes, todavía no estoy seguro. Digamos que es infinito para este ejemplo.)
Entonces:
Pero a veces el «…» se puede usar en el medio para guardar escribir listas largas:
Ejemplo: el conjunto de letras:
{a, b, c, .. ., x, y, z}
En este caso es un conjunto finito (sólo hay 26 letras, ¿no?)
Conjuntos numéricos
Entonces, ¿qué tiene esto que ver con las matemáticas? Cuando definimos un conjunto, todo lo que tenemos que especificar es una característica común. ¿Quién dice que «no podemos hacerlo con números?
Y así sucesivamente. Podemos crear diferentes tipos de conjuntos.
También podemos definir un conjunto por sus propiedades, como {x | x > 0} que significa «el conjunto de todas las x», de modo que x es mayor que 0 «, consulte Notación del generador de conjuntos para obtener más información.
Y podemos tener conjuntos de números que no tienen una propiedad común, simplemente se definen de esa manera. Por ejemplo:
{4, 5, 6, 10, 21}
{2, 949, 48282, 42882959, 119484203 }
Son todos los conjuntos que simplemente golpeé aleatoriamente en mi teclado para producir.
¿Por qué son importantes los conjuntos?
Los conjuntos son la propiedad fundamental de las matemáticas. Ahora, como advertencia, los conjuntos, por sí mismos, parecen bastante inútiles. Pero es solo cuando aplicamos conjuntos en diferentes situaciones que se convierten en el poderoso bloque de construcción de las matemáticas que son.
Las matemáticas pueden complicarse increíblemente bastante rápido. Teoría de gráficos, álgebra abstracta, análisis real, complejo Análisis, álgebra lineal, teoría de números y la lista continúa. Pero hay una cosa que todos estos comparten en común: conjuntos.
Conjunto universal
 |
Al principio usamos la palabra «cosas» entre comillas. A esto lo llamamos el conjunto universal. Es un conjunto que contiene todo. Bueno, no exactamente todo. Todo lo que sea relevante para nuestra pregunta. |
|
 |
En la teoría de números, el conjunto universal son todos los enteros, ya que la teoría de números es simplemente el estudio de números enteros. |
|
 |
Pero en Cálculo (también conocido como análisis real), el conjunto universal son casi siempre los números reales. |
|
 |
Y en el análisis complejo, lo adivinó, el conjunto universal son los números complejos. |
Más notación
 |
Cuando se habla de conjuntos, es bastante estándar usar letras mayúsculas para representar el conjunto y letras minúsculas para representar un elemento en ese conjunto. Por ejemplo, A es un conjunto y a es un elemento nt en A. Lo mismo con B y b, y C y c. |
Ahora no tiene que escuchar el estándar , puedes usar algo como m para representar un conjunto sin romper ninguna ley matemática (cuidado, puedes obtener π años en la cárcel de matemáticas por dividir entre 0), pero esta notación es bastante agradable y fácil de seguir, ¿por qué no?
Además, cuando decimos que un elemento a está en un conjunto A, usamos el símbolo ![]() para mostrarlo.
para mostrarlo.
Y si algo no está en un set use ![]() .
.
Ejemplo: el conjunto A es {1,2,3}. Podemos ver que 1 ![]() A, pero 5
A, pero 5 ![]() A
A
Igualdad
Dos conjuntos son iguales si tienen precisamente el mismos miembros. Ahora, a primera vista, puede que no parezcan iguales, por lo que es posible que tengamos que examinarlos de cerca.
Ejemplo: ¿Son A y B iguales donde:
- A es el conjunto cuyos miembros son los primeros cuatro números enteros positivos
- B = {4, 2, 1, 3}
Comprobemos. Ambos contienen 1. Ambos contienen 2. Y 3, Y 4. Y hemos verificado todos los elementos de ambos conjuntos, así que: ¡Sí, son iguales!
Y el signo igual ( =) se usa para mostrar igualdad, por lo que escribimos:
A = B

Subconjuntos
Cuando definimos un conjunto, si tomamos partes de ese conjunto, podemos formar lo que se llama un subconjunto.
En general:
A es un subconjunto de B si y solo si cada elemento de A está en B.
Así que usemos esta definición en algunos ejemplos.
Intentemos un ejemplo más difícil.
Subconjuntos adecuados
Si miramos la definición de subconjuntos y dejamos que nuestra mente divague un poco, llegamos a un extraño conclusión.
Sea A un conjunto. ¿Están todos los elementos de A en A?
Bueno, umm, por supuesto, ¿verdad?
Eso significa que A es un subconjunto de A. ¡Es un subconjunto de sí mismo!
Esto no parece muy apropiado, ¿verdad? Si queremos que nuestros subconjuntos sean adecuados, introducimos (qué más, sino) subconjuntos adecuados:
A es un subconjunto adecuado de B si y solo si cada El elemento de A también está en B, y existe al menos un elemento en B que no está en A.
Esta pequeña pieza al final está ahí para asegurarse de que A no sea un subconjunto adecuado de sí mismo: decimos que B debe tener al menos un elemento adicional.
Ejemplo:
{1, 2, 3} es un subconjunto de {1, 2, 3}, pero no es un subconjunto adecuado de {1, 2, 3}.
Ejemplo:
{1, 2, 3} es un subconjunto adecuado de {1, 2, 3, 4} porque el elemento 4 no está en el primer conjunto.
Observe que cuando A es un subconjunto adecuado de B, también es un subconjunto de B.
Aún más notación
Cuando decimos que A es un subconjunto de B, escribimos A ![]() B.
B.
O nosotros puede decir que A no es un subconjunto de B por A ![]() B («A no es un subconjunto de B»)
B («A no es un subconjunto de B»)
Cuando hablamos de subconjuntos adecuados, eliminamos la línea de abajo y se convierte en A ![]() B o si queremos decir lo contrario, A
B o si queremos decir lo contrario, A ![]() B.
B.
Conjunto vacío (o nulo)
Esto es probablemente lo más extraño de los conjuntos.

Como ejemplo, piense en el conjunto de teclas de piano de una guitarra.
«¡Pero espere!», dice: «No hay teclas de piano en una guitarra. guitarra! «
Y tienes razón. Es un conjunto sin elementos.
Esto se conoce como Conjunto Vacío (o Conjunto Nulo). No hay elementos en él. Ni uno. Cero.
Se está representado por ![]()
O por {} (un conjunto sin elementos)
Algunos otros ejemplos del conjunto vacío son el conjunto de países al sur del polo sur.
Entonces, ¿qué tiene de extraño el conjunto vacío? Bueno, esa parte viene a continuación.
Conjunto y subconjuntos vacíos
Así que volvamos a nuestra definición de subconjuntos. Tenemos un conjunto A. No lo definiremos de ninguna manera más que eso, podría ser cualquier conjunto. ¿Es el conjunto vacío un subconjunto de A?
Volviendo a nuestra definición de subconjuntos, si cada elemento del conjunto vacío también está en A, entonces el conjunto vacío es un subconjunto de A. Pero, ¿qué pasa si ¿no tiene elementos?
Se necesita una introducción a la lógica para entender esto, pero esta afirmación es una «vacuidad» o «trivialmente» cierta.
Una buena forma de pensar es: no podemos encontrar ningún elemento en el conjunto vacío que no esté en A, así que debe ser que todos los elementos en el conjunto vacío estén en A.
Entonces, la respuesta a la pregunta planteada es un rotundo sí.
El conjunto vacío es un subconjunto de cada conjunto, incluido el conjunto vacío en sí.
Orden
No, no el orden de los elementos. En conjuntos, no importa en qué orden estén los elementos.
Ejemplo: {1,2,3,4} es el mismo conjunto que {3,1,4,2}
Cuando decimos orden en conjuntos nos referimos al tamaño del conjunto.
Otro nombre (mejor) para esto es cardinalidad.
Un conjunto finito tiene un orden finito (o cardinalidad). Un conjunto infinito tiene un orden infinito (o cardinalidad).
Para conjuntos finitos, el orden (o cardinalidad) es el número de elementos.
Ejemplo: {10, 20, 30, 40} tiene un orden de 4.
Para conjuntos infinitos, todo lo que podemos decir es que el orden es infinito. Curiosamente, podemos decir con conjuntos que algunos infinitos son más grandes que otros, pero este es un tema más avanzado en conjuntos.
¡Arg! ¡No más notación!
No, es broma. No más notación.
de
y