Oppimistavoitteet
- Ilmoita de Broglien aaltoyhtälö.
- Käytä tämä yhtälö liikkuvan objektin aallonpituuden laskemiseksi.
Bohrin mallin ulkopuolella
Bohrin atomimalli oli arvokas osoittamaan kuinka elektronit pystyivät absorboimaan ja vapauttamaan energiaa ja kuinka atomien emissiospektrit luotiin. Malli ei kuitenkaan todellakaan selittänyt, miksi elektronien pitäisi olla vain kiinteillä pyöreillä kiertoradoilla sen sijaan, että ne kykenisivät olemaan rajattomassa määrässä kiertoratoja, joilla kaikilla on erilaisia energioita. Selittääkseen miksi atomienergiatilat kvantisoidaan, tutkijoiden oli mietittävä uudelleen tapaa, jolla he tarkastelivat elektronin luonnetta ja sen liikettä.
Planckin tutkimus kuumien kohteiden emissiospektreistä ja myöhemmät tutkimukset valosähköisestä vaikutuksesta olivat osoittaneet, että valo kykeni käyttäytymään sekä aallona että hiukkasena. Tuntui järkevältä miettiä, voisivatko elektronit olla myös kaksoisaaltopartikkeliluonteisia. Vuonna 1924 ranskalainen tiedemies Louis de Broglie (1892–1987) johti yhtälön, joka kuvasi minkä tahansa hiukkasen aaltoluonnetta. Erityisesti minkä tahansa liikkuvan kohteen aallonpituus (λ) saadaan:
\ displaystyle \ lambda = \ frac {h} {mv}
Tässä yhtälössä h on Planckin vakio , m on hiukkasen massa kg: na ja v on hiukkasen nopeus m / s. Alla oleva ongelma osoittaa, kuinka elektronin aallonpituus lasketaan.
Jos laskisimme 40 m / s: n nopeudella heitetyn 0,145 kg: n pesäpallon aallonpituuden, keksimme äärimmäisen lyhyen aallonpituus luokkaa 10−34 m. Tätä aallonpituutta on mahdotonta havaita edes edistyneillä tieteellisillä laitteilla. Vaikka kaikki kohteet liikkuvat aaltomaisella liikkeellä, emme koskaan huomaa sitä, koska aallonpituudet ovat aivan liian lyhyitä. Toisaalta hiukkaset, joilla on mitattavat aallonpituudet, ovat kaikki hyvin pieniä. Elektronin aaltoluonne osoittautui kuitenkin avaintekijäksi uudessa ymmärryksessä elektronin luonteesta. Elektroni, joka on rajoitettu tiettyyn tilaan atomin ytimen ympärillä, voi liikkua kyseisen atomin ympäri vain siten, että sen elektroniaalto ”sopii” atomin kokoon oikein. Tämä tarkoittaa, että elektroniaaltojen taajuudet kvantisoidaan. E = hv-yhtälön perusteella kvantisoidut taajuudet tarkoittavat, että elektronit voivat esiintyä atomissa vain tietyillä energioilla, kuten Bohr oli aiemmin teorioinut.
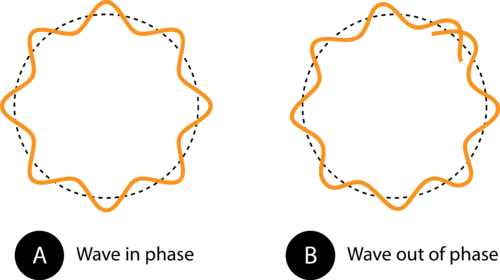
Kuva 1. Kiertoradan ympärysmitta kohdassa (A) antaa elektroniaallon sopia täydellisesti kiertoradalle. Tämä on sallittu kiertorata. Kohdassa (B) elektroniaalto ei mahtuu oikein kiertoradalle, joten kiertorata ei ole sallittu.
Yhteenveto
- DeBroglie-aaltoyhtälöt mahdollistavat minkä tahansa liikkuvan aallonpituuden laskemisen. esine.
- Kun elektronin nopeus pienenee, sen aallonpituus kasvaa.
Harjoittele
Käytä linkkiä alla harjoitellaksesi laskutoimituksia deBroglie-aaltoyhtälö:
http://science.widener.edu/svb/tutorial/debrogliecsn7.html
tarkistus
- mitä eikö Bohr-malli selittänyt?
- Ilmoita deBroglien aaltoyhtälö.
- Mitä tapahtuu, kun elektronin nopeus pienenee?