A Poincaré-sejtést és további 6 komplex matematikai elméletet a Clay Mathematics Institute (CMI) Millenniumi Díj-problémáknak nevezte el. Mindegyik problémát “fontos klasszikus kérdésnek írták le, amely az évek során ellenállt a megoldásoknak”, és az első ember, aki megoldást talált a CMI jóvoltából 1 000 000 dolláros keresetre. Amint azonban fentebb látta, a problémák megoldása nem egyszerű feat. Az egyik probléma megoldatlan maradt, amióta Bernhard Riemann német matematikus 1859-ben megfogalmazta.
A fent említett német matematikusról elnevezett Riemann-hipotézist széles körben a tiszta megoldatlanul legfontosabb problémának tartják matematika. A számelmélet iránt nagyon érdekes, mert a prímszám eloszlásával kapcsolatos eredményeket tartalmaz, amelyeket a biológiától kezdve a titkosításon és a kvantummechanikán keresztül mindenben alkalmaznak. A Riemann-hipotézis megértéséhez először meg kell magyaráznunk néhány kulcsot fogalmak:
- Egy komplex szám a + bi alakú, ahol i-t i² = -1 határozza meg. Ebben a formában a komplex szám valós része a, és a képzeletbeli rész bi.
- A Riemann zeta függvény egy komplex változó (a komplex számok függvénye) függvénye, amelyet az alábbi egyenlet határoz meg: ahol s bármely 1-től eltérő komplex szám, és amelynek értékei szintén összetettek:
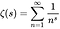
- A függvény “nulla” olyan x, hogy f (x) = 0
- A Riemann zeta függvény “triviális nullái” negatív páros egész számok (-2, -4, -6,…)
- A “nem triviális nullák” A Riemann zeta függvény s értéke az összes többi s értéke, amelyekre ζ (s) = 0 (azaz. s nem negatív páros egész szám).
Most, hogy néhány definíciónk van lefelé, folytathatjuk a Riemann-hipotézist:
A Riemann zeta függvény minden nem triviális nulla valós része 1/2
Ez (nekem legalábbis) sokkal könnyebben érthető, mint a Poincaré-sejtés, és intuitívan nem tűnik túl nehéznek. Úgy tűnik azonban, hogy ez sem jelent sokat. Tényleg, kit érdekel, ha ennek a véletlenszerű függvénynek az értéke 0. Nos, nem meglepő, hogy sok matematikus igen, és nagyon jó okból.
Néhány számnak megvan az a különleges tulajdonsága, hogy nem fejezhető ki két kisebb szám szorzataként (szorzat szorzat), azaz. 2,3,5,7,11, stb. Prímszámként ismertek, bizonyos értelemben a legegyszerűbb számok, amiket kaphatunk, és ezek alkotják az összes többi szám építőköveit. Frusztráló módon azonban úgy tűnik, hogy a prímszámok semmilyen mintát nem követnek. A 3137 prímszám, és az utána következő csak 3163-ig következik, majd a 3167 és a 3169 gyors egymásutánban következik, amelyek mindegyike prím. Dióhéjban, ha talál egy prímszámot, akkor nem lehet megmondani, hogy hol lesz a következő, anélkül, hogy közben ellenőrizné az összes számot. A prímszám-tétel (PNT) használatával azonban megtudhatja, hogy hány prímszám van egy bizonyos küszöb alatt.
A prímszám-tétel csak egy becslés, különböző értékek más valószínűséggel adják meg a létezést. helyes, de soha nem 100% -os bizonyosság. Azonban értse meg azt a feltételezést, hogy a Reimann-hipotézis igaz, létrehozhat egy matematikai közelítést, amely egyesíti a Prímszám-tételt és a Riemann-zéta függvény nem triviális nulláit, hogy hibajavítsa a belső komponenseket, biztosítva a “lehető legjobbat” a prímszám-tétel hibaterme. Ha a Reimann-hipotézist teljesen be lehetne bizonyítani, ez lehetővé tenné a PNT számára, hogy hihetetlenül szoros becsléseket nyújtson a tényleges értékhez, sok lehetőséget nyitva meg a matematika különböző ágaiban. sok fontos hipotézis létezik, amelyek szerint “Ha a Riemann-hipotézis igaz, akkor …”, tehát ennek a problémának a megoldása azonnal érvényesíteni fogja az összes következő sejtést is.