Most, hogy megtanulta az egész számok szorzását, az egész számok felosztásának szélnek kell lennie. Ennek oka az, hogy ugyanazokat a szabályokat követik.
szabályok az egész számok felosztásáról
1. lépés: Osszuk el abszolút értékeiket.
2. lépés: Határozzuk meg a végső válasz (hányadosként ismert) előjelét a következő feltételekkel.
- 1. feltétel: Ha a két szám előjele megegyezik, a hányados mindig pozitív szám.
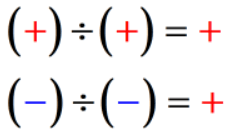
- 2. feltétel: Ha a két szám jelei különböznek, a hányados mindig negatív szám.
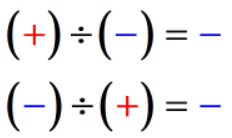
Példák az egész tagolásra
1. példa: Ossza fel az alábbi két egész számot.
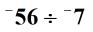
Megoldás: Először keresse meg a két egész szám abszolút értékét.
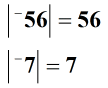
Ezután ossza fel a számokat, vagy keresse meg hányadosukat .
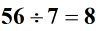
Végül határozza meg a válasz vagy hányados végső előjelét. Mivel két egész számot osztunk azonos előjellel, a hányadosnak pozitív előjele lesz.
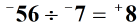
2. példa: Ossza fel az alábbi két egész számot.
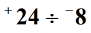
Megoldás: Osszuk el a két egész szám abszolút értékeit.
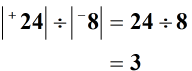
A fenti szabályok betartása mellett egész számok felosztásakor különböző aláírja, hogy a végleges válasz (hányados) negatív.
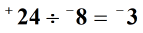
3. példa: Oszd el az alábbi három egész számot balról jobbra
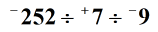
Megoldás: Három vagy több egész szám felosztásához fontos, hogy az osztási műveletet balról jobbra végezzük. Ezenkívül meg tudjuk valósítani úgy, hogy egyszerre két egész számot osztunk. A zárójel mutatja az első két egész számot, amelyet fel kell osztani, és bármi is legyen az eredmény vagy hányados, el fogjuk osztani a következővel. Tehát itt van, – 252 + 7-gyel elosztva egyenlő – 36. Ez negatív hányados, mivel két különböző előjelű egész számot osztunk fel. Ezután vesszük ezt a hányadost, és osszuk el a következő egész számmal. –36 ÷ –9 = + 4-et kapunk.
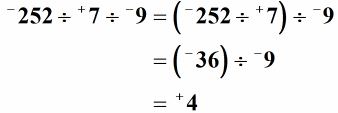
Gyakorlás a munkalapokkal
Ezenkívül érdekelhet:
Egész szám hozzáadása
Egész kivonás
Egész szorzás