Mi a standard deviáció? | STDEV.P | STDEV.S | Variancia
Ez az oldal elmagyarázza, hogyan lehet kiszámítani a szórást a teljes sokaság alapján az Excel STDEV.P függvényével, és hogyan lehet megbecsülni a szórást egy minta alapján az Excel STDEV.S függvényével.
Mi a szórás?
A szórás olyan szám, amely megmondja, hogy a számok milyen messze vannak az átlaguktól.
1. Például az alábbi számok átlagos (átlag) értéke 10.
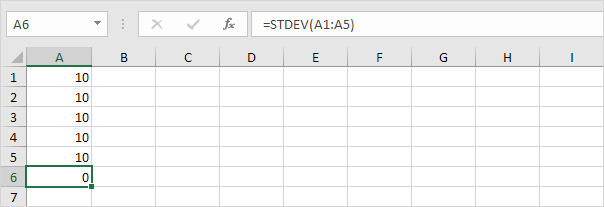
Magyarázat: A számok megegyeznek azt jelenti, hogy nincs változás. Ennek eredményeként a számok szórása nulla. Az STDEV függvény régi függvény. A Microsoft Excel az új STEDV.S függvény használatát javasolja, amely pontosan ugyanazt az eredményt adja.
2. Az alábbi számok átlaga (átlaga) 10 is.
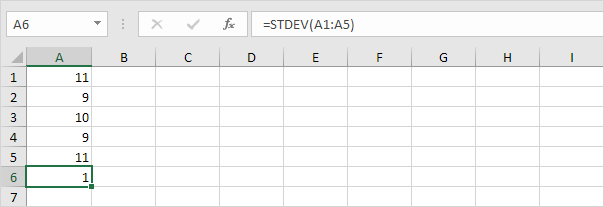
Magyarázat: A számok közel vannak az átlaghoz. Ennek eredményeként a számoknak alacsony a szórása.
3. Az alábbi számok átlaga (átlaga) 10 is.
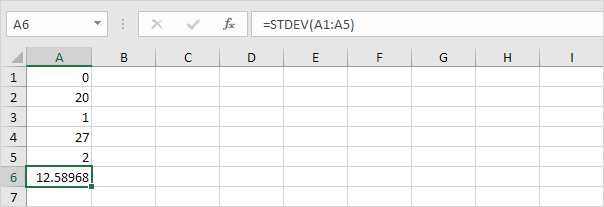
Magyarázat: a számok el vannak osztva. Ennek eredményeként a számoknak nagy a szórása.
STDEV.P
Az STDEV.P függvény (a P jelentése populáció) az Excelben kiszámítja a szórást a teljes populáció alapján. Például 5 tanulóból álló csoportot tanít. Megvan az összes hallgató teszt pontszáma. A teljes populáció 5 adatpontból áll. Az STDEV.P függvény a következő képletet használja:
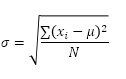
Ebben a példában x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (átlag), N = 5 (adatpontok száma).
1. Számítsa ki az átlagot (μ).
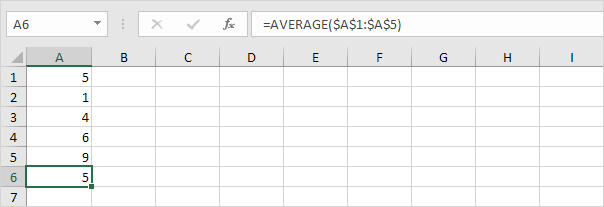
2. Számítsa ki minden számhoz az átlagtól való távolságot.
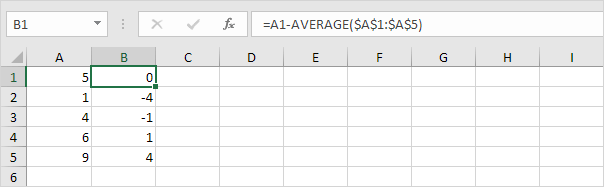
3. Minden számnál jelölje be ezt a távolságot.
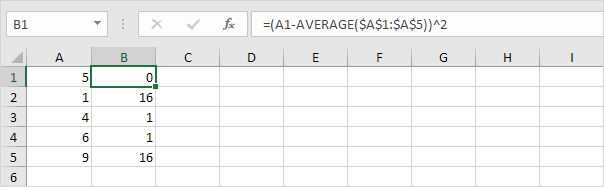
4. Összegezze (∑) ezeket az értékeket.
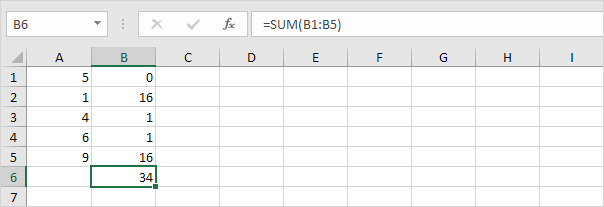
5. Osszuk el az adatpontok számával (N = 5).
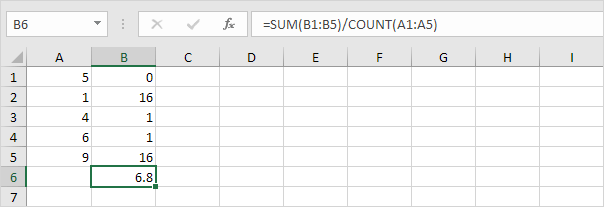
6. Vegyük a négyzetgyököt.
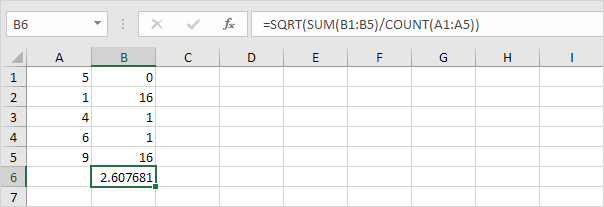
7. Szerencsére az Excel STDEV.P függvénye elvégezheti ezeket a lépéseket az Ön számára.
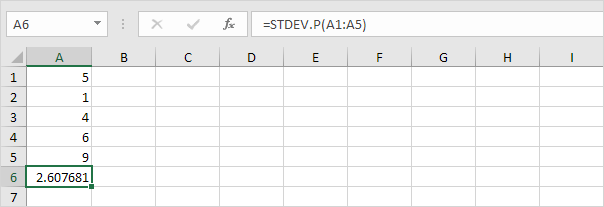
STDEV.S
Az STDEV.S függvény (az S jelentése Minta) az Excelben becsli a szórást egy minta alapján. Például egy nagy diákcsoportot tanít. Csak 5 tanuló teszt pontszáma van. A minta nagysága 5. Az STDEV.S függvény a következő képletet használja:
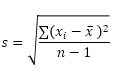
Ebben a példában x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (ugyanazok a számok, mint fent), x̄ = 5 (minta átlag), n = 5 (minta mérete).
1. Ismételje meg a fenti 1–5. lépéseket, de az 5. lépésben ossza el N-1 értékkel N. helyett.
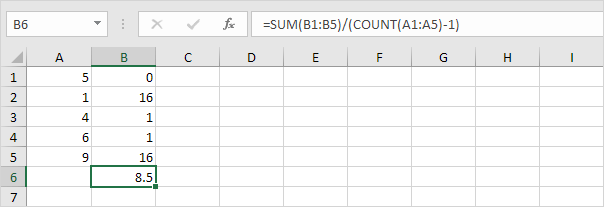
2. Vigye a négyzetgyöket.
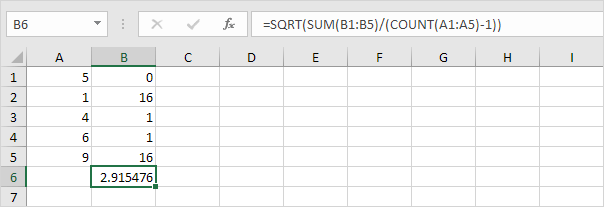
3. Szerencsére az Excel STDEV.S függvénye elvégezheti ezeket a lépéseket az Ön számára.
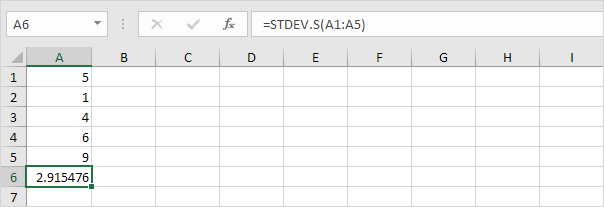
Megjegyzés: miért osztunk fel n – 1 helyett n, ha egy minta alapján megbecsüljük a szórást? Bessel korrekciója szerint az n-1 helyett n-el osztva jobban megbecsülhető a szórás.
Variancia
A variancia a szórás négyzete. Olyan egyszerű. Néha könnyebb a varianciát használni a statisztikai problémák megoldásakor.
1. Az alábbi VAR.P függvény a teljes sokaság alapján kiszámítja a varianciát.
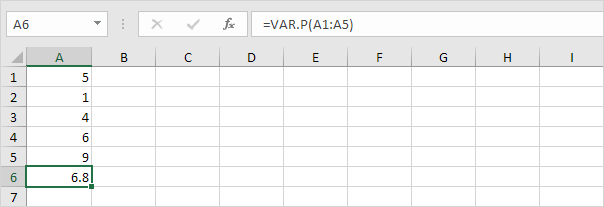
Megjegyzés: ezt a választ már tudta (lásd: 5. lépés az STDEV.P alatt). Vegyük ennek az eredménynek a négyzetgyökét, hogy megtaláljuk a szórást a teljes népesség alapján.
2. Az alábbi VAR.S függvény egy minta alapján becsüli meg a varianciát.
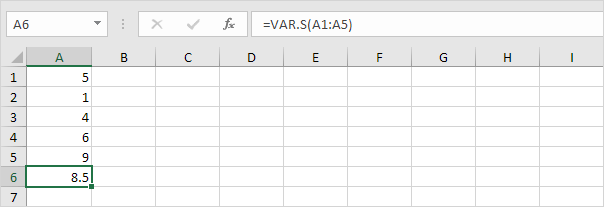
Megjegyzés: ezt a választ már tudta (lásd a lépést) 1 alatt STDEV.S). Vegyük ennek az eredménynek a négyzetgyökét, hogy a minta alapján megtaláljuk a szórást.
3. A VAR és a VAR.S pontosan ugyanazt az eredményt adja.
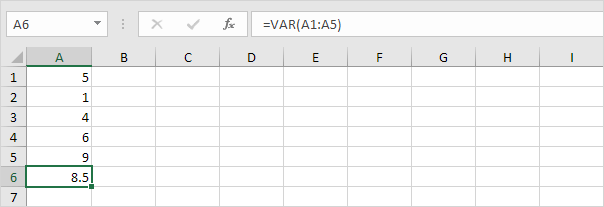
Megjegyzés: A Microsoft Excel az új VAR.S függvény használatát javasolja.