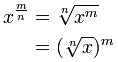Más néven “radikálisok” vagy “racionális kitevők”
teljes szám kitevői
Először nézzük meg a teljes számot kitevők:

A szám kitevője megmondja, hányszor kell használni a számot szorzásban.
Ebben a példában: 82 = 8 × 8 = 64
Másik példa: 53 = 5 × 5 × 5 = 125
Töredékes kitevő
De mi van akkor, ha a kitevő tört?
|
A 12-es kitevő valójában négyzetgyök A 13-as kitevő kocka gyökér A 14-es kitevő a 4. gyökér És így tovább! |
 |
Miért?
Lássák “miért” példa.
Először is, a kitevők törvényei megmondják, hogyan kell kezelni a kitevőket, ha szorzunk:
Példa: x2x2 = (xx) (xx) = xxxx = x4
Ami azt mutatja, hogy x2x2 = x (2 + 2) = x4
Próbáljuk meg ezt tört töredékű kitevőkkel:
Próbálkozzon másik frakcióval
Próbáljuk meg újra, de egynegyed (1/4) kitevővel:
Példa:
16¼ × 16¼ × 16¼ × 16¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Tehát a szorzatban négyszer használt 16¼ 16-ot ad,
és így a 16¼ egy 16-os gyökér 4. gyökere
Általános szabály
½-nél működött, worked-vel működött, sőt általában véve működik:
x1 / n = Az x
n-edik gyöke
Tehát előállhatunk ezzel:
| |
|
Példa: Mi az a 271/3?
Válasz: 271/3 = ![]() 27 = 3
27 = 3
Mi a helyzet a bonyolultabb törtekkel?
Mi a helyzet egy olyan tört kitevővel, mint a 43/2?
Ez azt jelenti, hogy egy kockát (3) és egy négyzetgyököt (1/2) bármilyen sorrendben kell csinálni.
A tört (például m / n) két részre bontható:
- egy egész számrész (m) és
- egy törtrész (1 / n) rész
Tehát, mivel m / n = m × (1 / n), ezt megtehetjük:
A sorrend nem számít, tehát m / n = (1 / n) × m esetén is működik:
És ezt kapjuk:
| |
|
Néhány példa:
példa : Mi az a 43/2?
43/2 = 43 × (1/2) = √ (43) = √ (4 × 4 × 4) = √ (64) = 8
vagy
43/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 8
Mindkét esetben ugyanaz az eredmény.
Példa: Mi az a 274/3?
274 / 3 = 274 × (1/3) = ![]() (274) =
(274) = ![]() (531441) = 81
(531441) = 81
vagy
274/3 = 27 (1/3) × 4 = (![]() 27) 4 = (3) 4 = 81
27) 4 = (3) 4 = 81
Minden bizonnyal könnyebb volt a 2. út!
Most … Játssz a grafikonnal!
Nézd meg, milyen gördülékenyen változik a görbe, amikor a törtekkel játszol Ez az animáció megmutatja, hogy ez a töredékes kitevők ötlete remekül illeszkedik egymáshoz:
Kipróbálandó dolgok:
- Kezdje m = 1 és n = 1 értékekkel, majd lassan növelje n úgy, hogy láthassa az 1/2, az 1/3 és az 1/4
- Ezután próbálja meg az m = 2 értéket, majd csúsztassa n felfelé és lefelé olyan töredékek megtekintéséhez, mint a 2/3 stb. Most próbálja meg a -1 kitevőt
- Végül próbálja meg növelni az m értéket, majd csökkenteni az n értéket, majd csökkenteni az m értéket, majd növelni az n értéket: a görbének körbe és körbe kell mennie