Analisi costo-volume-profitto

L’analisi Costo-Volume-Profitto (CVP) è una tecnica di contabilità gestionale che studia l’effetto del volume delle vendite e dei costi del prodotto sull’utile operativo di un’azienda. Mostra come l’utile operativo è influenzato dalle variazioni dei costi variabili, dei costi fissi, del prezzo di vendita per unità e del mix di vendita di due o più prodotti.

L’analisi CVP si occupa dell’identificazione dei costi fissi di un’azienda , il suo costo variabile per unità, il prezzo del suo prodotto e l’utilizzo di questi dati per elaborare le seguenti misure:

• Margine di contribuzione: la differenza tra i ricavi totali di un’azienda e i costi variabili totali. È l’importo con cui le vendite contribuiscono ai costi fissi e al profitto.
• Margine di contribuzione per unità: la differenza tra il prezzo di vendita e il costo variabile per unità.
• Rapporto del margine di contribuzione: il rapporto tra margine di contribuzione sul totale dei ricavi.
• Punto di pareggio: il volume delle vendite (in unità e dollari) in cui l’azienda non sta subendo perdite né guadagnando alcun profitto.
• Vendite con reddito target: il livello di vendite necessario per raggiungere un reddito target.
• Margine di sicurezza: la percentuale (o in dollari) di cui il volume delle vendite di un’azienda supera il suo punto di pareggio.

l’input più critico nell’analisi CVP è la relazione tra i diversi costi e volume, ovvero la classificazione dei costi in categorie fisse e variabili.

Equazione dell’analisi CVP

La relazione fondamentale costo-volume-profitto può essere derivato dall’equazione del profitto:

Profitto = Entrate – Costi fissi – Costi variabili

Dove il profitto è PR, il ricavo è uguale al prodotto del prezzo per unità P e del volume delle vendite in unità Q , i costi fissi FC sono costanti e i costi variabili totali sono pari al prodotto delle unità vendute Q e del costo variabile per unità V, la seguente equazione è una rappresentazione più elaborata delle relazioni CVP:

PR = Q × P – Q × V – FC

Questa è l’equazione più fondamentale che può essere utilizzata per lavorare molti numeri CVP.

Per pausa -un punto, dobbiamo impostare PR ad 0 e risolvere per Q e otteniamo:

Break-even Q = FC ÷ (P – V)

Mostra che break- il punto pari può essere calcolato dividendo il costo fisso per il margine di contribuzione per unità.

Approccio all’equazione del margine di contribuzione

L’equazione CVP discussa sopra può anche essere espressa in termini di margine di contribuzione del prodotto:

PR = Q × P – Q × V – FC

PR = Q × (P – V) – FC

(P – V) nell’equazione sopra è il margine di contribuzione per unità.

Grafico CVP

La relazione CVP può anche essere espressa sotto forma di un grafico chiamato grafico CVP:

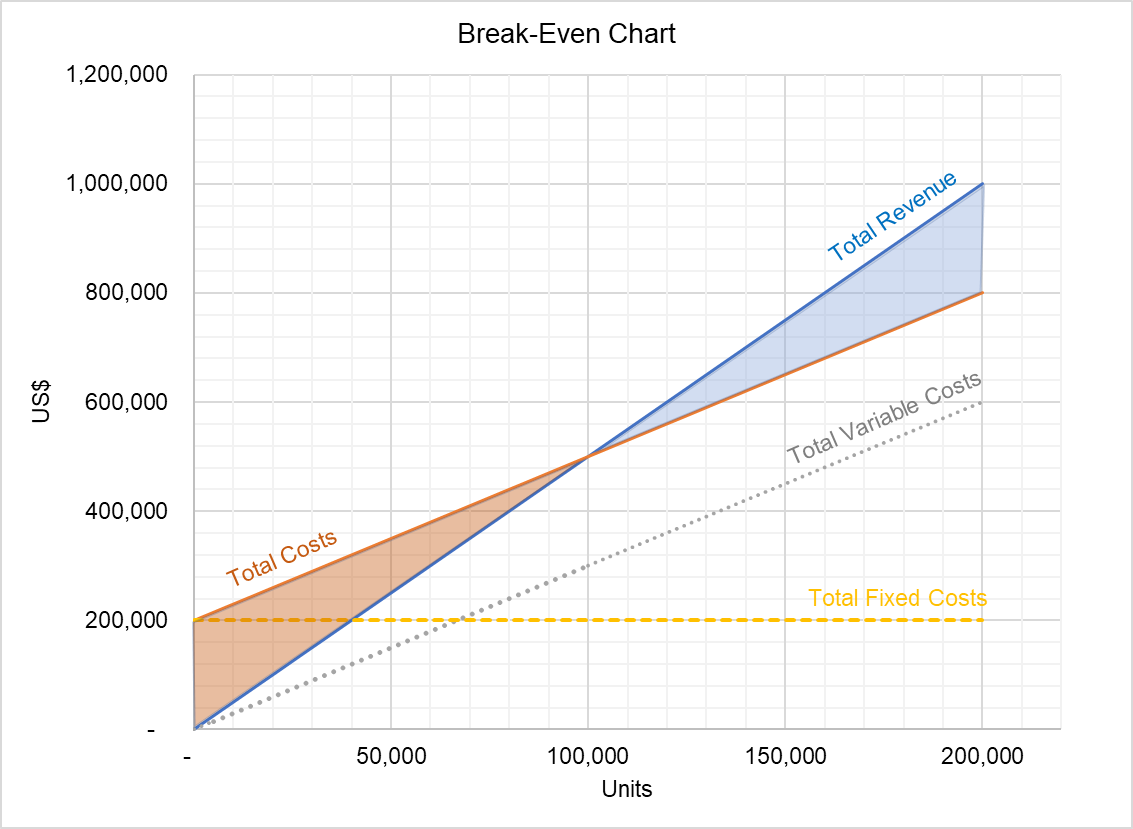
Il grafico sopra mostra la relazione tra entrate totali e costi totali. L’area tra le due linee sotto il punto di pareggio rappresenta le perdite e l’area sopra il punto di pareggio mostra il volume del profitto totale. Questo grafico può essere utilizzato per identificare i profitti a diversi livelli di output.

Presupposti dell’analisi CVP

Anche se l’analisi CVP è uno strumento di contabilità gestionale utile, le sue conclusioni sono valide solo quando i seguenti presupposti trattenere:

• Tutti i costi possono essere classificati come variabili o fissi. A tal fine, i costi misti vengono suddivisi in componenti variabili e fisse utilizzando tecniche quali il metodo alto-basso, il metodo del grafico a dispersione e l’analisi di regressione.
• Il prezzo di vendita per unità, il costo variabile per unità e il costo fisso totale sono costanti . Questa ipotesi è problematica a causa dell’esistenza di economie di scala, rendimenti di scala crescenti / decrescenti e effetto della curva di apprendimento.
• Tutti i ricavi e i costi hanno una relazione lineare con il volume.
• Le vendite il mix di una società rimane costante.

di Irfanullah Jan, ACCA e ultima modifica il 2 ottobre 2020