Che cos’è la deviazione standard? | DEV.ST.P | STDEV.S | Varianza
Questa pagina spiega come calcolare la deviazione standard in base all’intera popolazione utilizzando la funzione DEV.ST.P in Excel e come stimare la deviazione standard in base a un campione utilizzando la funzione DEV.ST.s. in Excel.
Cos’è la deviazione standard?
La deviazione standard è un numero che ti dice quanto sono lontani i numeri dalla loro media.
1. Ad esempio, i numeri seguenti hanno una media (media) di 10.
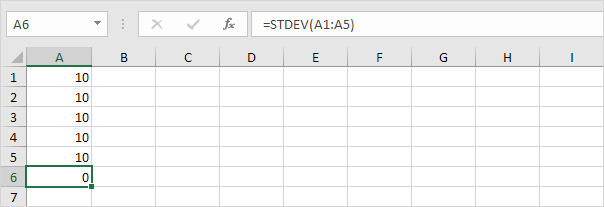
Spiegazione: i numeri sono tutti uguali che significa che non ci sono variazioni. Di conseguenza, i numeri hanno una deviazione standard pari a zero. La funzione DEV.ST è una vecchia funzione. Microsoft Excel consiglia di utilizzare la nuova funzione STEDV.S che produce lo stesso risultato.
2. Anche i numeri seguenti hanno una media (media) di 10.
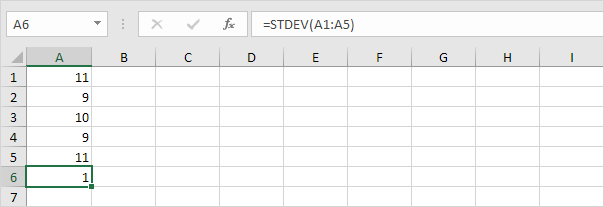
Spiegazione: i numeri sono vicini alla media. Di conseguenza, i numeri hanno una deviazione standard bassa.
3. Anche i numeri seguenti hanno una media (media) di 10.
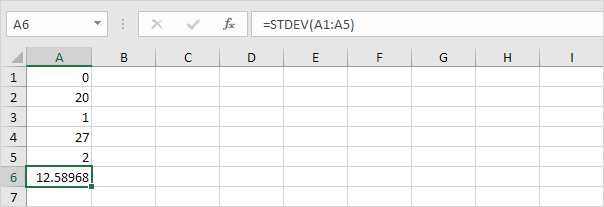
Spiegazione: i numeri sono distribuiti. Di conseguenza, i numeri hanno una deviazione standard elevata.
DEV.ST.P.
La funzione DEV.ST.P (la P sta per Popolazione) in Excel calcola la deviazione standard in base all’intera popolazione. Ad esempio, stai insegnando a un gruppo di 5 studenti. Hai i punteggi dei test di tutti gli studenti. L’intera popolazione è composta da 5 punti dati. La funzione DEV.ST.P utilizza la seguente formula:
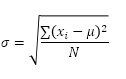
In questo esempio, x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9, μ = 5 (media), N = 5 (numero di punti dati).
1. Calcola la media (μ).
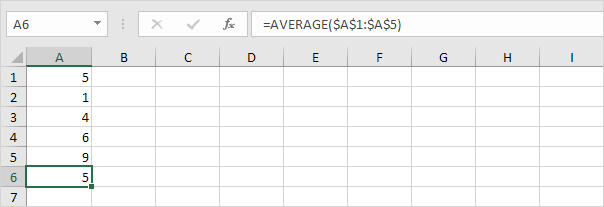
2. Per ogni numero, calcola la distanza dalla media.
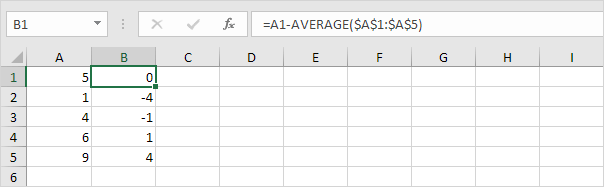
3. Per ogni numero, quadrare questa distanza.
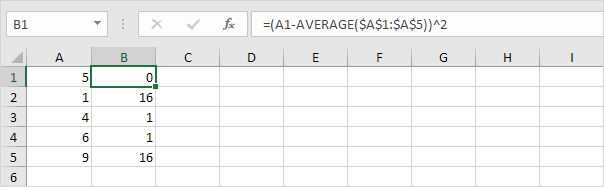
4. Somma (∑) questi valori.
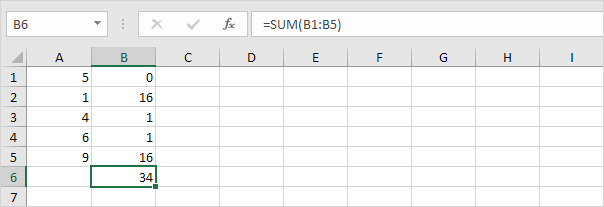
5. Dividi per il numero di punti dati (N = 5).
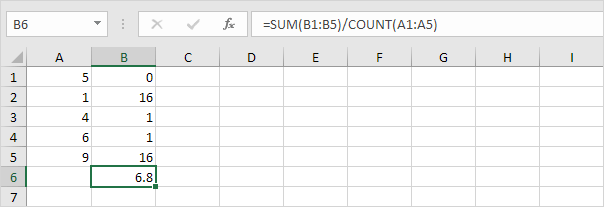
6. Prendi la radice quadrata.
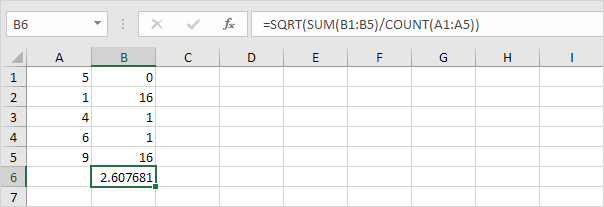
7. Fortunatamente, la funzione DEV.ST.P in Excel può eseguire tutti questi passaggi per te.
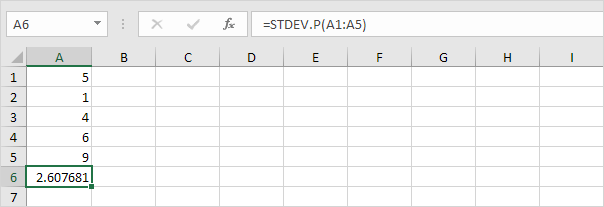
DEV.ST./h3>
La funzione DEV.ST.ST (la S sta per Sample) in Excel stima la deviazione standard in base a un campione. Ad esempio, stai insegnando a un grande gruppo di studenti. Hai solo i punteggi del test di 5 studenti. La dimensione del campione è uguale a 5. La funzione DEV.ST.s. utilizza la seguente formula:
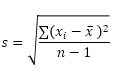
In questo esempio, x1 = 5, x2 = 1, x3 = 4, x4 = 6, x5 = 9 (stessi numeri come sopra), x̄ = 5 (campione media), n = 5 (dimensione del campione).
1. Ripeti i passaggi 1-5 precedenti ma al passaggio 5 dividi per n-1 invece di N.
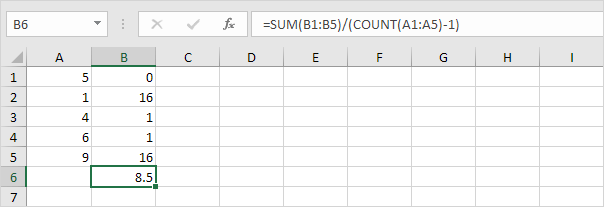
2. Prendi la radice quadrata.
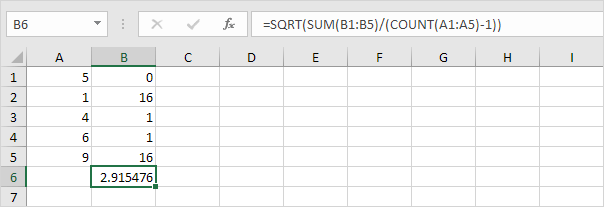
3. Fortunatamente, la funzione DEV.ST.ST in Excel può eseguire tutti questi passaggi per te.
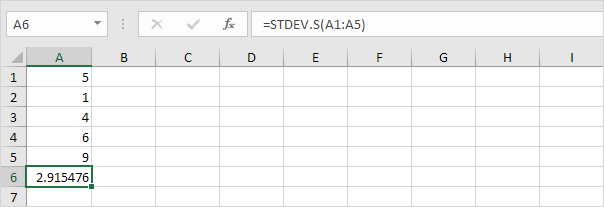
Nota: perché dividiamo per n – 1 invece di n quando stimiamo la deviazione standard in base a un campione? La correzione di Bessel afferma che la divisione per n-1 invece che per n fornisce una stima migliore della deviazione standard.
Varianza
La varianza è il quadrato della deviazione standard. È così semplice. A volte è più facile usare la varianza quando si risolvono problemi statistici.
1. La funzione VAR.P di seguito calcola la varianza in base all’intera popolazione.
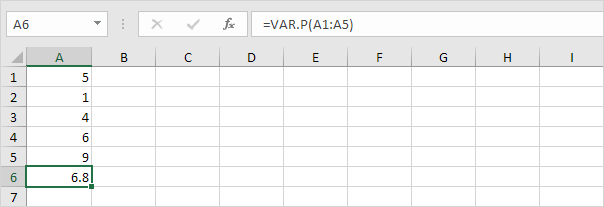
Nota: conoscevi già questa risposta (vedi passaggio 5 in DEV.ST.P). Prendi la radice quadrata di questo risultato per trovare la deviazione standard basata sull’intera popolazione.
2. La funzione VAR.S di seguito stima la varianza in base a un campione.
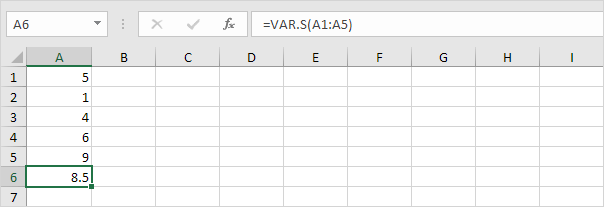
Nota: conoscevi già questa risposta (vedi passaggio 1 sotto STDEV.S). Prendi la radice quadrata di questo risultato per trovare la deviazione standard basata su un campione.
3. VAR e VAR.S producono lo stesso identico risultato.
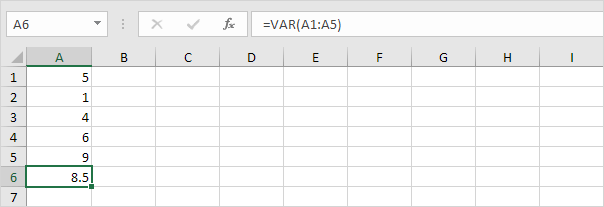
Nota: Microsoft Excel consiglia di utilizzare la nuova funzione VAR.S.